Semantic Argument Method
Suppose we want to prove the validity of a propositional logic formula  .
Several methods to do this exists, one of which is called the semantic argument method.
.
Several methods to do this exists, one of which is called the semantic argument method.
We start the proof by assuming that a falsifying interpretation exists:
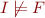
and try to show that this leads to a contradiction by applying semantic definitions of the logical connectives.
Thus, we obtain a set of proof rules:
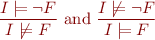
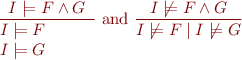
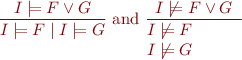
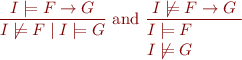
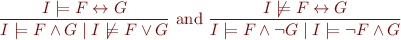
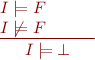
Extension to First-order logic
The proof rules above apply in addition to the following proof rules for the quantifiers:
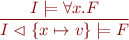
for any  in the domain of the interpretation.
in the domain of the interpretation.
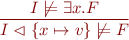
for any  in the domain of the interpretation.
in the domain of the interpretation.
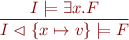
for a fresh  in the domain of the interpretation.
in the domain of the interpretation.
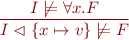
for a fresh  in the domain of the interpretation.
in the domain of the interpretation.