Simple QE for Integer Difference Inequalities
Language of Less-Than-Equals Over Integers
Consider language: 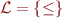 and the theory of structure
and the theory of structure  where
where
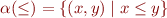
Lemma: This theory does not admit quantifier elimination.
Proof.
Suppose the theory admits quantifier elimination.
What is the quantifier-free formula equivalent to
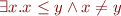
It is formula with one free variable,  .
So it must be built out of atomic formulas
.
So it must be built out of atomic formulas  and
and  , and is therefore it is either always true or always false, regardless of the value of
, and is therefore it is either always true or always false, regardless of the value of  . It thus cannot be equivalent to the above formula.
. It thus cannot be equivalent to the above formula.
End.
So  must be expressible. Let us extend the language: consider theory in language
must be expressible. Let us extend the language: consider theory in language 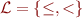 with
with  interpreted as
interpreted as  on integers.
on integers.
Does the theory of this structure admit quantifier elimination?
Consider quantifier-free formula 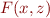 equivalent to
equivalent to

Extending the Language
Language: 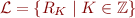
Theory of structure  where
where
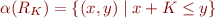
Note that 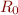 is the less-than-equal relation on integers.
is the less-than-equal relation on integers.
In other words, we look at the language of this syntax, where  is the set of variables:
is the set of variables:
F ::= A | (F&F) | (F|F) | ~F | ALL V.F | EX V.F A ::= v=v | v + K ≤ v | true | false K ::= ... -2 | -1 | 0 | 1 | 2 | ...
Equality is expressed by 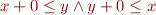
Quantifier Elimination in the Extended Language
Quantifier elimination for this language is similar to Simple QE for Dense Linear Orders.
What is 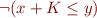 equivalent to?
equivalent to?
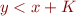

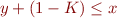
What are conjunctions of literals equivalent to?
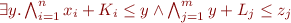
How do we eliminate existential quantifier?
Using 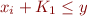 and
and 
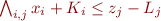
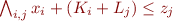
Example
Prove:
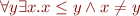

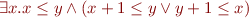


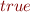
If we apply this technique to a closed formula in this theory, what formulas do we obtain as a result?