Proving Invariants Containing Relations
Simplified version of the example from a quiz.
r1 = r k = 0 W = {} while //: W = range(r \ r1) (r1 != {}) { v1 = lookup(k,r1) W = W union v1 r1 = r1 \ ({k} x v1) }
Note that this program does not mention integers. In fact, the fact that  is integer is not important for partial correctness, only for termination.
However, it can be helpful to know that we could assume the first and the second components of
is integer is not important for partial correctness, only for termination.
However, it can be helpful to know that we could assume the first and the second components of  to be disjoint.
to be disjoint.
Postcondition of v1=lookup(k,r1) implies, among others:
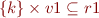
Indeed, this holds when 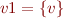 because then
because then 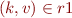 . When
. When 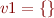 , then the condition trivially holds.
, then the condition trivially holds.
Note that the negation of  is
is
 .
.
The negation of the verification condition that implies that invariant is preserved has (among others) the following conjuncts:
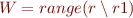 (assume invariant)
(assume invariant)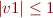 ,
,  (postcondition of lookup)
(postcondition of lookup) (loop body)
(loop body) (loop body)
(loop body)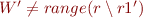 (asserting invariant–note that VC is negated)
(asserting invariant–note that VC is negated)
Now translate the operations on sets and relations into first-order logic, by introducing
- unary predicates for
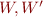
- binary predicates for
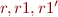
and identifying sets and relations with the corresponding predicates.
We translate each conjunct into first-order logic.
Clause 1
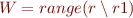
Note that, for all  ,
,

We obtain

which decomposes into implication from right to left:
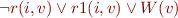
and the implication left to right:
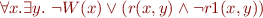
that Skolemizes and decomposes into two clauses:
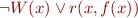
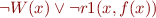
Note that the Skolem function in the original problem maps indices into results of the array. If we worked in many-sorted logic, we could assume that it has type 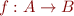 for two incompatible types
for two incompatible types 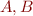 where
where 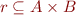 and
and  . This means that expressions such as
. This means that expressions such as 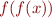 are not meaningful and restricts Herbrand universe. See the paper Decidable fragments of many-sorted logic.
are not meaningful and restricts Herbrand universe. See the paper Decidable fragments of many-sorted logic.
Clause 2
v1 is a set which is singleton, so we can add the axiom
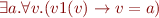
and we Skolemize  . Note that we do not claim
. Note that we do not claim 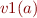 , since it could be empty.
, since it could be empty.
Then
 (postcondition of lookup)
(postcondition of lookup)
becomes
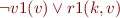
Clause 3
 (loop body)
(loop body)
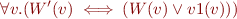
That is, from left to right:
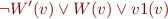
and from right to left:
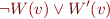
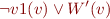
Clause 4
 (loop body)
(loop body)
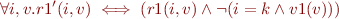
and this decomposes further.
Clause 5
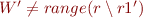


So we obtain another Skolem constant, b and negation of equivalence. Equivalence is false iff at least one side is true and at least one is false, so we obtain
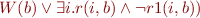
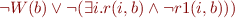
In the first case we obtain another Skolem constant i1 and two clauses:
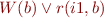

In the second case we obtain the clause:
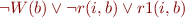
Summary
Variables 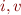 are universally quantified,
are universally quantified, 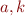 are constants,
are constants,  is function symbol:
is function symbol:
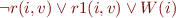
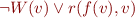
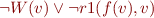
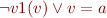
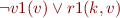
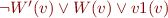
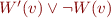
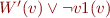
- …
We obtain many, but finitely many clauses. Moreover, if we respect typing constraints, we obtain a finite Herbrand universe.
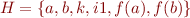
So we just need to instantiate the universally quantified clauses with those values (respecting types will further help).
Note that we need to consider cases where  and the cases where
and the cases where  .
.
Universal Class
Whenever Herbrand model (in unsorted or many-sorted sense) is finite, Herbrand theorem gives us a decision procedure for this logic.
One such class are formulas that have no function symbols, and where existentials appear only at the top level. This is so-called “effectively propositional logic” (EPR), or the Bernays-Schoenfinkel-Ramsey class of first-order logic.
This class can encode, for example, formulas that talk about relations with set algebra operations, because those operations give either universal quantifiers or top-level existential quantifiers.