LARA

Pre-Computation of post in Predicate Abstraction

There is an alternative definition, which can be used to convert the above problem into a finite-state exploration problem. (It will be particularly useful if we consider an extension from conjunctions to disjunction of conjunctions.)

The condition

\begin{equation*} \forall x,y,x',y'.\ (\bigwedge_{P\in a} P(x,y)) \land R(x,y,x',y') \rightarrow P'(x',y') \end{equation*}

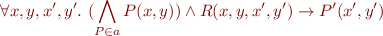
is equivalent to the validity of the formula

\begin{equation*} (\bigwedge_{P\in a} P) \rightarrow wp(R, P') \end{equation*}

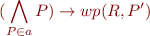
Fix a predicate 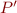$P'$. Consider all $a \subseteq {\cal P}$ for which the above condition holds, define them as

\begin{equation*} suf(R,P') = \{ a \mid (\bigwedge_{P\in a} P) \rightarrow wp(R, P') \} \end{equation*}

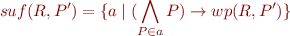
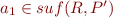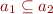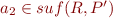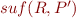Clearly, if $a_1 \in suf(R,P')$ and $a_1 \subseteq a_2$, then also $a_2 \in suf(R,P')$. So, we can represent $suf(R,P')$ using its minimal elements 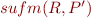$sufm(R,P')$. These are minimal sufficient sets of predicates that ensure that 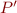$P'$ holds.

Then, we can define equivalently

\begin{equation*} sp^\#(a,R) = \{ P' \mid \exists a' \in sufm(R,P').\ a' \subseteq a \} \end{equation*}

The advantage of this definition is that we compute 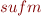$sufm$ for a given predicate 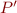$P'$ and command given by 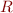$R$, and then we can efficiently compute $sp^{\#}$ for all abstract values $a$ by checking inclusion of finite sets.

Approximation: The set 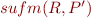$sufm(R,P')$ can have up to 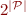$2^{|{\cal P}|}$ elements. To avoid this, we can restrict it to only those subsets $a'$ that have at most e.g. 3 predicates.

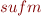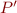Note that using smaller $sufm$ means that some $a'$ will be missing, the condition will be false in some cases, and in those cases $P'$ will not be included in the postcondition, so the resulting abstract element will be larger in the lattice. So the approach is still correct, just not as precise.