Analyses Based on Formulas
Many analyses can be viewed in this way.
Fixpoint Approach
Let the domain be the set of quantifier-free formulas of some logic, ordered by implication
Is this a partial order? We would need to do a quotient construction to obtain it.
Non-existence of limits: infinite disjunction need not be a formula of our logic, e.g. consider formulas on linear arithmetic and take the limit
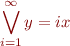
In general, a logic that can represent exact least upper bounds needs to express the conditions such as “there exists a sequence of statements that produces the given state”.
Approximation
Rule for computing formula (called 'fact') in step  at program point
at program point 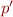
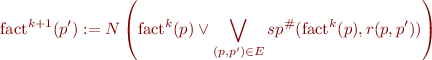
where  is some approximation function. This is analogous to Abstract interpretation recipe.
is some approximation function. This is analogous to Abstract interpretation recipe.
Here the goal of  is to ensure termination (and efficiency). The essential condition is that
is to ensure termination (and efficiency). The essential condition is that
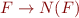
is a valid formula.
One generic approch: use a syntactic widening.
View formula as a conjunction. Then define
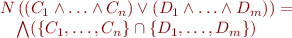
Why are there no infinite chains when using such  ?
?
To make it less syntactic: deduce some consequences of the conjunction (taken from a finite set):
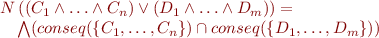
where
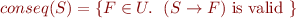
where  is some class of useful formulas.
is some class of useful formulas.
References
- Safety Checking of Machine Code described induction iteration method (wp instead of sp)
- analysis based on sets in the Hob analysis system
Constraint-Based Approach
Give up least fixpoint requirement (it is approximation anyway).
Search for any fixpoint - it will be a set of loop invariants:
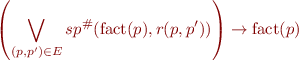
Works better if we also have postconditions and assertions that need to be satisfied (otherwise we may come up with trivial invariants).
Assume a 'template' for the invariant, e.g. (Karr's analysis) each fact is a linear equation  on program variables
on program variables  .
.
The condition for loop invariants gives a system of equations on coefficients 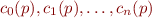 for each of the finitely many program points
for each of the finitely many program points  .
.
If there exists a solution, this gives an invariant.
X := 10
Y := 0
while (X >= 0) {
X := X-1
if random() { Y = Y+1 }
}
Invariant of the form 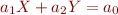 .
.

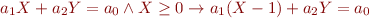

Such equations need to hold for all values of  ,
, , which gives constraints on
, which gives constraints on 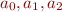 that can be solved based on properties of real fields (linear programming, Farkas lemma).
that can be solved based on properties of real fields (linear programming, Farkas lemma).
Thanks to quantifier elimination for real fields, the technique extends to polynomial invariants as well.
If there is no solution, there is no invariant of that particular template form.
Note: for non-numerical domains, we obtain different kinds of constraints. A popular class are set constraints.
References
- Calculus of Computation Textbook, Chapter 12