Transition System and Collecting Semantics
 - program counter values. Denoted
- program counter values. Denoted 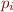 (program point) or
(program point) or  (vertex in CFG)
(vertex in CFG)
 - values of other variables
- values of other variables
Transition system semantics:
- state is set of pairs
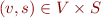
- element of concrete lattice is a set of such pairs
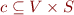 , i.e.
, i.e. 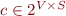
- post maps set of such pairs to an extended set of such pairs,
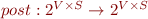
Collecting Semantics
Take 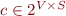 .
.
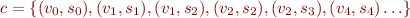
Because  is an arbitrary set, for a given
is an arbitrary set, for a given  , there can be any number of
, there can be any number of 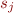 such that
such that 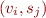 is in
is in  (in fact,
(in fact,  is a relation on
is a relation on  ).
).
We can equivalently represent this relation 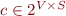 as the following multi-valued function, by grouping all
as the following multi-valued function, by grouping all 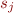 for a given
for a given  :
:
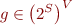
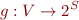
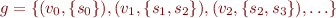
Collecting semantics simply works with 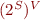 instead of
instead of 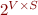 , which is just notational change.
, which is just notational change.
- lattice element is a function
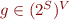 i.e.
i.e. 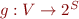
- we have function
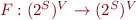 that transforms such functions and directly corresponds to
that transforms such functions and directly corresponds to 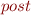
Control-flow graph: 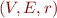 where
where
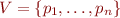 is set of program points
is set of program points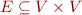 are control-flow graph edges
are control-flow graph edges 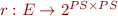 , so each
, so each 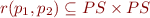 is relation describing the meaning of command between
is relation describing the meaning of command between 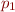 and
and 
Compute the big relation on global states in terms of  and
and 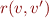 .
.
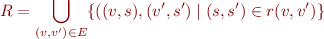
Then derive a nice expression for 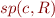 where
where 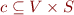 .
.
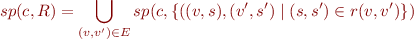
Now we come back to the definition of post, which was
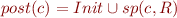
so we obtain
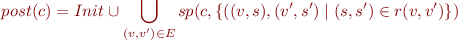
Now instead of 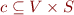 , consider
, consider 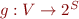 , and define a new sp on such different representation. Then
, and define a new sp on such different representation. Then
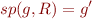
where
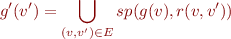
We also represent  as
as  , then we obtain function
, then we obtain function  that corresponds to
that corresponds to  :
:
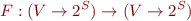
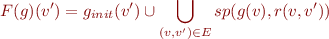
Note that 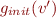 will be
will be  except at the entry into our control-flow graph.
except at the entry into our control-flow graph.
If we compute 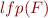 , we obtain
, we obtain 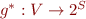 such that
such that 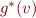 gives precisely the set of all reachable states at a program point
gives precisely the set of all reachable states at a program point  . Such
. Such  is isomorphic to
is isomorphic to 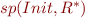 .
.
We call this way of defining  the collecting semantics of the
program, because it collects all states for each program point. It
will be convenient to define how abstract interpretation works.
the collecting semantics of the
program, because it collects all states for each program point. It
will be convenient to define how abstract interpretation works.