Termination and Efficiency of Abstract Interpretation Analysis
Definition: A chain of length  is a sequence
is a sequence 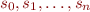 such that
such that
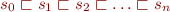
where  means, as usual,
means, as usual, 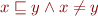
Definition: A partial order has a finite height  if it has a chain of length
if it has a chain of length  and every chain is of length at most
and every chain is of length at most  .
.
A finite lattice is of finite height
Example: The constant propagation lattice 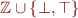 is an infinite lattice of height 2. One example chain of length 2 is
is an infinite lattice of height 2. One example chain of length 2 is

Here the  function is given by
function is given by
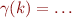 when
when 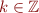
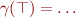
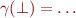
The ordering is given by 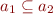 iff
iff 
Example: If a state of a (one-variable) program is given by an integer, then a concrete lattice element is a set of integers. This lattice has infinite height. There is a chain
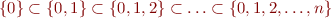
for every  .
.
Convergence in Lattices of Finite Heignth
Consider a finite-height lattice 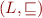 of height
of height  and function
and function
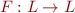
What is the maximum length of sequence 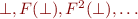 ?
?
Give an effectively computable expression for 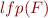 .
.
Computing the Height when Combining Lattices
Let 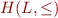 denote the height of the lattice
denote the height of the lattice 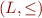 .
.
Product
Given lattices 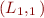 and
and 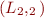 , consider product lattice with set
, consider product lattice with set  and potwise order
and potwise order
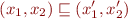
iff 
What is the height of the product lattice?
Exponent
Given lattice 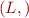 and set
and set  , consider the lattice
, consider the lattice 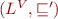 defined by
defined by
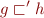
iff 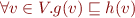 .
.
What is the height of the exponent lattice?
Answer: height of  times the cardinality of
times the cardinality of  .
.