Intuition for Parallel and Iterative Updates

Consider a function 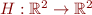$H : \mathbb{R}^2 \to \mathbb{R}^2$

This function can be given by two component functions 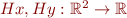$Hx,Hy : \mathbb{R}^2 \to \mathbb{R}$ , one for each result component of the pair:

$\begin{equation*} H(x,y) = (Hx(x,y), Hy(x,y)) \end{equation*}$

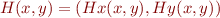
Consider an imperative program that iterates $H$ . We could write it like this, where we compute the values for next iteration first and then update them:

while (iter < max) {
  xNext = Hx(x,y)
  yNext = Hy(x,y)
  x = xNext
  y = yNext
  iter = iter + 1
}

Or, we could write it iteratively like this:

while (iter < max) {
  x = Hx(x,y)
  y = Hy(x,y)
  iter = iter + 1
}

As max is increasing, do these two loops behave the same? Can one converge and the other not? Given examples.