Homework 01

Part 1

Here are the questions for the first (theoretical) part of the homework.
Homework 1 - Loop invariants

Here is an example proof of an inductive invariant, your proof for Problem 1 should be of similar formality.

Please type up your answer and submit it through the submission form on Moodle that will appear shortly.
The deadline is Friday, 4th March.

Part 2

The goal of the second part is to get familiar with writing algorithms on trees in scala. For this you need to complete the code given in the following scala source file.
Homework 1 - Quantifier elimination for QBF
In this file you will find several function skeletons that you need to complete in order to decide the validity, satisfiability, and equivalence of QBF formulas using quantifier elimination.

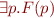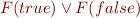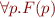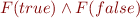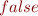Quantifier elimination for propositional logic replaces subformula $\exists p. F(p)$ by $F(true) \lor F(false)$ and replaces $\forall p. F(p)$ by $F(true) \land F(false)$ . Your goal here is to implement this transformation, and then also simplify formula by eliminating 'true' and 'false' whenever possible, replacing e.g. $true \land p$ with $p$ , and $false \land p$ with $false$ .homework1_qbf.txt

The deadline for part 2 is March 8th.

Please upload your solutions through http://moodle.epfl.ch .