Trace Semantics

One way to describe the meaning of the program is to give a relation between initial and final states, a set of pairs 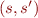$(s,s')$ such that executing program from $s$ reaches the final state $s'$ .

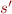Another way is to associate with a program a set of traces, e.g.

$\begin{equation*} s, a_1, s_1, a_2, s_2, \ldots, a_2, s_n, a', s' \end{equation*}$

which describe the entire execution sequence, with states $s$ and actions $a$ . This can be more convenient for expressing certain program properties

the order of invocation of certain program actions
behavior of concurrent programs (there is no way to describe interleavings in the model that omits all intermediate states!)

The elements of traces come from an infinite set in general. However, it is useful to consider abstraction of traces, where we preserve just names of actions (e.g. the sequence of names of procedures invoked).

Trace semantics can also be defined inductively or using fixpoints.