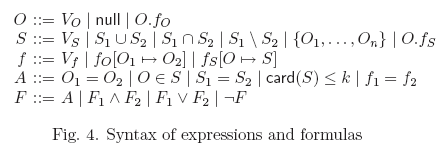LARA

Deciding a Language of Sets (and Relations)

Language

Consider a simple language of sets, motivated by verification of programs that manipulate containers:

Set-Valued Fields Motivation

Set-Valued Fields Logic

Question: how do we justify 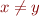$x \neq y$ ?

Idea of Decidability

We show that this language is decidable by reduction to universal class.

Convert formula to negation-normal form.

Express all operations using quantifiers.

Note: the resulting formula has a bounded number of universal quantifiers

  • this gives good complexity of the generated formulas (in NP if the constants are written in unary)

Reference