LARA

Using Relational Semantics

We next show how to use relational semantics to prove properties of specific programs, by checking relation subset.

We also apply relational semantics to prove two normal-form theorems about programs.

Proving Program Properties

A general approach:

  • compute semantics of a program as a mathematical object (e.g. relation)
  • prove that the relation satisfies the desired property

Example

Consider the code 

r = 0;
i = y;
while (i > 0) (
  r = r + x;
  i = i - 1
)

We represent it as 

r = 0;
i = y;
loop (
  assume (i > 0);
  r = r + x;
  i = i - 1
);
assume (i <= 0);

We compute the meaning of 

assume (i > 0);
r = r + x;
i = i - 1

as the relation $b$ whose formula is

\begin{equation*} i > 0 \land r' = r + x \land i' = i - 1 \end{equation*}

We then wish to compute the transitive closure $b^* = \bigcup_{n \ge 0} b^n$.

We claim that for every $n \ge 0$ relation $b^n$ is given by formula

\begin{equation*} i \ge n \land r' = r + n x \land i' = i - n \end{equation*}

We can prove this claim by induction. The union of these relations is then given by

\begin{equation*} \exists n \ge 0. i \ge n \land r' = r + n x \land i' = i - n \end{equation*}

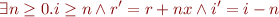
From there we can derive the meaning of 

r = 0;
i = y;
loop (
  assume (i > 0);
  r = r + x;
  i = i - 1
)

as

\begin{equation*} \exists n \ge 0. y \ge n \land r' = n x \land i' = y - n \end{equation*}

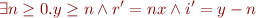
which when composed with assume($\neg (i > 0)$) = assume($i \leq 0$) gives

\begin{equation*} \exists n \ge 0. y \ge n \land r' = n x \land i' = y - n \land i' \leq 0 \end{equation*}

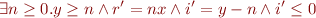
which is equivalent to

\begin{equation*} y \ge 0 \land i' = 0 \land r' = y x \end{equation*}

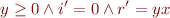
This is the semantics of the above code.

Relations as Specifications

Nondeterministic programs can be used to specify other programs

If $r$ is relation representing program and $s$ relation representing specification, we say that program meets specification iff

\begin{equation*} r \subseteq s \end{equation*}

Example:

This allows us to prove that programs satisfy their contracts, expressed using preconditions and postconditions: 

void f()
  requires x > 0
  ensures x > 0
{
  x = x + 1;
}

What is the relation for contract with

  • precondition $P(x)$
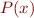
  • postcondition $Q(x)$

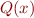
Answer: 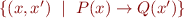$\{(x,x')\ \mid\ P(x) \rightarrow Q(x')\}$

The correctness condition:

\begin{equation*} \{ (v,v').\ v' = v + 1 \} \subseteq \{ (v,v').\ v > 0 \rightarrow v' > 0 \} \end{equation*}

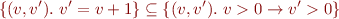
reduces to:

\begin{equation*} \forall v. \forall v'.\ v' = v + 1 \rightarrow ( v > 0 \rightarrow v' > 0) \end{equation*}

While Theorem

Definition: Control-Flow Graph (CFG) is graph 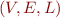$(V,E,L)$ where

  • $V$ is set of CFG nodes, representing program points
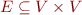  • $E \subseteq V\times V$ set of CFG edges (represent jumps)
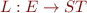  • $L : E \to ST$ gives a CFG statement for each edge
    • statements
    • conditions

Note: there are alternative representations

  • putting statements on nodes instead of edges
  • labelling outgoing edges

Transforming an example program to control flow graph.

We can describe the meaning of the program by writing one loop that traverses the control-flow graph.

Every program has a control-flow graph, so every program can be written using one loop.

The body of this loop is a relation, which we call transition relation. It can be described by the formula that has a particular form: disjunction of conjunctions, where each conjunction describes changes happening in one edge of the control-flow graph.

Normal Form for Loop-Free Programs

Example: 

(if (x < 0) x=x+1 else x=x);
(if (y < 0) y=y+x else y=y);

Without loops, after expressing conditionals using [] we obtain 

c ::=  x=T | assume(F) |  c [] c  |  c ; c

Laws:

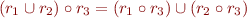
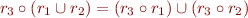
\begin{equation*} (r_1 \cup r_2) \circ r_3 = (r_1 \circ r_3) \cup (r_2 \circ r_3) \end{equation*}

\begin{equation*} r_3 \circ (r_1 \cup r_2) = (r_3 \circ r_1) \cup (r_3 \circ r_2) \end{equation*}

Using these laws, we can reduce each program in the syntax above into the following normal form:

\begin{equation*} \bigcup_{i=1}^n p_i \end{equation*}

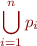
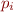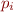Each $p_i$ is of form $b_1 \circ \ldots \circ b_k$ for some $k$, where each $b_i$ is assignment or assume. Each $p_i$ corresponds to one of the finitely paths from beginning to end of the acyclic control-flow graph for loop-free program.

Length of normal form with sequences of if-then-else can be exponential in the size of the program.

In general, we would like to postpone explicit enumeration of these paths as long as possible.