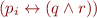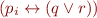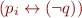Tseitin's Encoding

Definition: Formulas $F$ and $F'$ are equisatisfiable iff $F$ is satisfiable iff $F'$ is satisfiable.

Note: If a formula is satifiable, it is equisatisfiable with formula 'true'. If a formula is unsatisfiable, it is equisatisfiable with the formula 'false'.

Claim: each formula $F$ can be transformed in polynomial time into a new formula $F'$ such that $F$ is satisfiable iff $F'$ is satisfiable.

Procedure:

$\begin{equation*}\begin{array}{l} F\ \ \leadsto\ \ (p_i \leftrightarrow (q \land r)) \land subst(\{q \land r \mapsto p_i\},F) \\ F\ \ \leadsto\ \ (p_i \leftrightarrow (q \lor r)) \land subst(\{q \lor r \mapsto p_i\},F) \\ F\ \ \leadsto\ \ (p_i \leftrightarrow (\lnot q)) \land subst(\{(\lnot q) \mapsto p_i\},F) \\ \end{array} \end{equation*}$

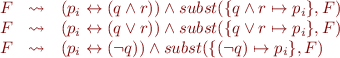
The use of last rule can be minimized by using negation-normal form–applying De Morgan's laws to push negation to leaves of the formula syntax tree.

Then transform each of the equivalences into a conjunction of clauses:

$(p_i \leftrightarrow (q \land r))$
$(p_i \leftrightarrow (q \lor r))$
$(p_i \leftrightarrow (\lnot q))$

Note: if $F$ is in negation-normal form, then we can replace some of these equivalences with implications.