LARA

Termination and Efficiency of Abstract Interpretation Analysis

Definition: A chain of length $n$ is a sequence 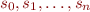$s_0, s_1, \ldots, s_n$ such that

\begin{equation*} s_1 \sqsubset s_2 \sqsubset \ldots \sqsubset s_n \end{equation*}

where $x \sqsubset y$ means, as usual, $x \sqsubseteq y \land x \neq y$

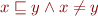
Definition: A lattice has a finite height $n$ if it has a chain of length $n$ and every chain is of length at most $n$.

A finite lattice is of finite height

Example: The constant propagation lattice 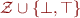${\cal Z} \cup \{\bot, \top\}$ is an infinite lattice of height 2. One example chain of length 2 is

\begin{equation*} \bot \sqsubset 42 \sqsubset \top \end{equation*}

Example: If a state of a (one-variable) program is given by an integer, then a concrete lattice element is a set of integers. This lattice has infinite height. There is a chain

\begin{equation*} \{ 0 \} \subset \{ 0, 1 \} \subset \{ 0, 1, 2 \} \subset \ldots \subset \{ 0, 1, 2, \ldots, n \} \end{equation*}

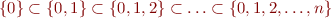
for every $n$.

Consider a finite-height lattice

Values at each program point in DataflowAnalysis.scala is monotonically increasing

  • stabilization happens in finite number of steps when the lattice has finite height
  • at each step the size of lattice in at least one point increases
    • termination in |CFG.V| |L.Elem| steps
    • in many cases can be shown to be better

Worklist Algorithm

The simple algorithm in DataflowAnalysis.scala always goes through all vertices

There is no need to go through vertices whose predecessors have not changed

Worklist algorithm:

  • maintain a worklist (queue) of vertices whose fact needs to be updated
  • initially: put entry into queue
  • remove a vertex from queue, compute its new fact
    • if the value changed, add all its successors into queue

Can avoid some unnecessary traversals

Note: we can re-order vertices in the queue

  • different orderings correspond to different algorithm variations
  • useful strategy: iterate over inner loops first