Sign Analysis as Symbolic Execution
Sign analysis performs Over-Approximation in symbolic execution
For variables 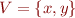 the symbolic state is:
the symbolic state is:
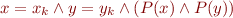
where 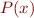 is one of the formulas
is one of the formulas  ,
,  ,
,  , or 'true' (and similarly for
, or 'true' (and similarly for 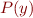 )
)
Initially, we approximate initial state (if unknown, then 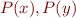 are true)
are true)
When we compute strongest postcondition, then we approximate it to obtain again formula in the previous form
Use a work-list algorithm to propagate symbolic state in the presence of loops
We go through loop several times until values stabilize
- illustration on our example