Mikaël Mayer
Program Synthesis
Program Synthesis Project presentation made thursday 28/05/2009 with Prezi.com
Program Synthesis - Toward Mathematically Generated Programs (report)
Problem definition and results
The program synthesis problem is about to find a function  such that
such that 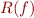 holds, where
holds, where 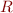 is a second-order logic predicate over functions.
is a second-order logic predicate over functions.
The question our algorithm tackles with is the following:
Given post and pre-condition and a set of axiomatic rules, generate a verified and terminating program which satisfies the post condition under the pre-conditions, plus eventually some more new pre-condition.
Formally :
Let P, Q two formulas.
The tool generates C and R such that
* {P^R} C {Q} holds for all initial values of variables and c terminates.
* C itself contains the verifiable proof that it is correct and that it terminates.
Example of automatically generated problems (18/05/2009 - 05/06/2009)
//! Sorting three integers
// Problem was solved in 62 steps
//{requires nothing else
if(c-b >= 0) {
if(b-a >= 0) {
z = c; y = b; x = a
} else {
if(c-a >= 0) {
z = c; y = a; x = b
} else {
z = a; y = c; x = b
}
}
} else {
if(c-a >= 0) {
z = b; y = c; x = a
} else {
if(b-a >= 0) {
z = b; y = a; x = c
} else {
z = a; y = b; x = c
}
}
}
//}ensures (({x,y,z}={a,b,c}&&(y >= x))&&(z >= y))
//! Verifying axioms with preconditions.
//! {((a <= 0) => F(a) = 0), ((a > 0) => F(a) = 1)} ? { x = F(y)}
if(-a > 0) {
x = 0
y = a
} else {
x = 1
y = a
}
24/05/2009
// The GCD problem
c = a
d = b
while(c != 0) {
// The GCD inner loop, code generated automatically
//!requires GCD(U,V+U)=GCD(U,V), GCD(U,V)=GCD(V,U), c>=0, d>=0, c!=0
if(-c+d >= 0) {
d' = -c+d; c' = c; x49 = c; x48 = d
} else {
c' = d; d' = c
}
//}ensures c'>=0, d'>=0, GCD(c',d')=GCD(c,d), (c', d')<(c, d)
c = c'; d = d'
}
// Here d contains gcd(a, b)
State of the project
The report and presentation have been done (see at the top).
You can consult the unreadable but almost always up-to-date Google Doc webpage on the draft of the project (until 2009/06).
We already :
We could :
We would like to make compelling applications such as :
Example : The GCD problem
The typical example we would like to be resolved is the GCD problem, which absolutely needs a loop.
Some axioms:
GCD(k*a, k*b) = k*GCD(a, b) GCD(a, b+k*a) = GCD(a, b) GCD(a, 0) = a GCD(a, b) = GCD(b, a)
Input:
Precondition: a >= 0, b >= 0 Postcondition: y = GCD(a, b)
A way to generate the program automatically
One Idea
In 2007, I realized an algorithm from this paper to decrypt sentences which were crypted by a letter permutation. For example:
"This sentence" => "Mogu unpmnpxn"
We assumed to know the language and had some dictionaries, and here is in one of the main decryption file.
In this past project:
- I spend almost three days with my binom to have clear specifications and modelization of the problem.
- I build the proofs and the program itself at the same time.
- The function that I worked on, and whose correctness and termination I proved, and in which there is a “huge” while loop with a lot of if/then/else, is named decryptoM
- I was able to prove that I never went into sentences like “throw new error” but I kept them, as they were useful during the proof construction.
- We were able to compare two programs, one entirely prooved and the other only made by hand, with the same specifications though. It appeared that the prooved program succeeded in everything in time, not the other one.
I was able to build the while loop from the specifications and the proof at the same time, so why not in the general case, to synthesize any program from specifications?
We are going to explore this way.
Potentially Useful References
Douglas R. Smith
see also earlier papers by the author bib
Sketching
Synthesis of Particular Algorithms
LTL Synthesis
In LTL synthesis we aim to build reactive finite state machines (FSM) from a given specification in Linear Temporal Logic (LTL). We assume that we have a given interface telling us the input and output signals of the desired FSM, e.g., our target machine should have two input signals x1 and x2 and two output signals y1 and y2. In every step, the machine reads values from the input signals and produces values at the output signals. (This is the reactive part.) Given a sequence of input values the system produces a corresponding sequence of output values. The specification tells which joined input-output sequences are desired.
LTL provides a convenient way to specify which input-output sequences defined a correct behavior. E.g., if you want to say that whenever the input x1 is set to 1, then the output y1 is set to 1 in the next step, you can write this as
G(x1=1 -> X(y1=1))
G stands for globally or always and X means in the next step. Another very useful property could be that the two outputs are never high at the same time, written in LTL you get G( !(y1=1 /\ y2=1)), where ! is the Boolean not-operator.
We have used LTL to specify and then automatically construct circuits (see pdf for more details). We also used LTL to locate and repair faults in small C-like programs (see pdf).
Predicate Abstraction and Synthesis
Boolean Repair paper (Bloem, Cook, …)
SETL
Classical Work on Stepwise Refinement
- Stepwise Program Derivation (and references in this paper, including Dijkstra, Morgan, Gries)
Program Specialization
- Partial evaluation book: http://www.itu.dk/people/sestoft/pebook/
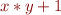 instead of
instead of 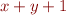 ? The first would satisfy conditions, but second not”)
? The first would satisfy conditions, but second not”)