Products of Lattices
Lattice elements can be combined into finite or infinite-dimensional vectors, and the result is again a lattice.
Lemma: Let 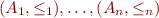 be partial orders. Define
be partial orders. Define 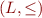 by
by
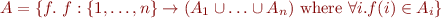
For 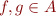 define
define

Then 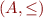 is a partial order. We denote
is a partial order. We denote 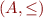 by
by
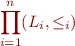
Moreover, if for each  ,
, 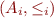 is a lattice, then
is a lattice, then 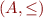 is also a lattice.
is also a lattice.
Note: for  a function
a function  with
with  ,
,  is isomorphic to an ordered pair
is isomorphic to an ordered pair 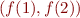 . We denote the product by
. We denote the product by
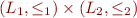 .
.
Example: Let 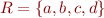 denote set of values. Let
denote set of values. Let 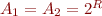 . Let
. Let

and let

Then we can define the product  . In this product,
. In this product,  iff:
iff:  and
and  . The original partial orders were lattices, so the product is also a lattice. For example, we have
. The original partial orders were lattices, so the product is also a lattice. For example, we have
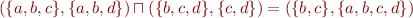
Collecting Semantics as example of products, fixpoints.