LARA

Problem 0

Review the Exercises 06 and solve the following exercises:

Answer the remaining questions from the Problem 3 c) that were not answered during the exercise session, namely: Is 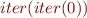$iter(iter(0))$ a fixpoint of $f$? Is $f$ an $\omega$-continuous function?

Problem 1

Define a monotonic function 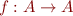$f : A \to A$ such that, for every natural number $k$, the value 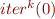$iter^k(0)$ is not a fixpoint of $f$.