Frame Conditions and Invariants
Motivation for Frame Conditions (Modifies Clauses)
Example procedure with globals x,y,z which increments x.
var x,y,z :: int;
proc inc()
requires y >= 0
ensures y = old(y) + 1
{ y = y + 1; }
proc test()
{
y = 0;
x = 2;
inc();
assert(x==2);
}
By rules so far in verification of test we consider
proc test()
{
y = 0;
x = 2;
var y1 = y;
assert(y >= 0);
havoc(x,y,z);
assume(y = y1 + 1);
assert(x==2);
}
More precise postcondition:
Problems:
- long to write
- specification must change every time we add variables
Frame condition notation
proc inc()
requires y >= 0
modifies y
ensures y = old(y) + 1
{ y = y + 1; }
Note: no mention of x,z.
Meaning is the same as above.
Translation when analyzing procedure call:
Meaning of Frame Conditions as Variable Lists
In general, for modifies clause
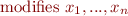
and the set of variables  , the 'ensures' clause receives additional postcondition
, the 'ensures' clause receives additional postcondition
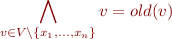
Global Invariants as Shorthands
If we write
invariant I(x,y)
it means that the formula I(x,y) is implicitly conjoined with precondition and postcondition of each procedure in the program.
For example,
invariant x <= y & 0 <= x
means that x,y are non-negative and y is greater or equal to x, before and after each procedure invocation.
Consequence: the invariant must hold before and after each procedure call as well.
Issues with Explicit Modifies Clauses
Using explicit modifies clauses in ListReverse.java
- must 'havoc' entire field, later restrict changes
- instantiable structures: using reachability to describe what was changed
- breaking encapsulation
Idea: use specification variables to make things simpler