Instead of computing the sequence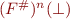 
for
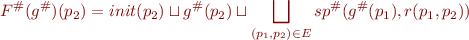
we can just as well compute the sequence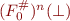 
where we omit the old values:
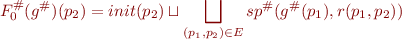
(In both cases we also include the initial set of states for the entry program point, they can be represented as special incoming edges.)
Lemma: Function 
is monotonic and
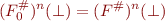
Proof:
Monotonicity follows from the monotonicity of 
, which follows from properties of 
, 
. By induction we then obtain
for all 
. From there by induction it follows
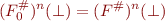
for all .
End of proof.
