Congruence Closure Algorithm and Correctness
Congruences on all Ground Terms
Let  be a set of ground equalities and disequalities representing the formula
be a set of ground equalities and disequalities representing the formula
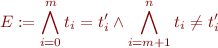
Then the following are equivalent:
 is satisfiable
is satisfiable- there exists a congruence on ground terms in which
 is true
is true  is true in the least congruence
is true in the least congruence  containing
containing 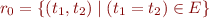
Congruences on Ground Terms Occurring in the Formula
Instead of a congruence on the (typically infinite) set of all ground terms, we compute congruences on the set  of the ground terms ocurring in
of the ground terms ocurring in  .
.
Note that 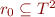 and that applying reflexivity, symmetry, transitivity keeps the relation in
and that applying reflexivity, symmetry, transitivity keeps the relation in  .
.
We need modify congruence condition to apply only to terms in  , using the following congruence condition:
, using the following congruence condition:
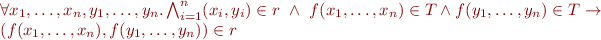
Algorith:
- start with
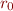
- apply the congruence rule above as well as reflexivity, symmetry and transitivity until the fixpoint
- denote result by
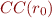 .
.
Theorem: conjunction of formulas in  is satisfiable iff for each
is satisfiable iff for each 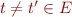 we have
we have 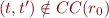 .
.
Proof:
- for each pair
 we have that
we have that  is a semantic consequence of
is a semantic consequence of 
- we use
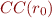 to construct a structure in which
to construct a structure in which  holds
holds- take as domain the equivalence classes of
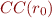 ; let
; let ![Math $[t]$](/w/lib/exe/fetch.php?media=wiki:latex:/imgfd1c70476e0dc90405de52861f9b3ab9.png) denote the equivalence class of
denote the equivalence class of 
- define
![Math $f([t_1],\ldots,[t_n])$](/w/lib/exe/fetch.php?media=wiki:latex:/img996b6d99744fa47e3613aca03da4c0df.png) as
as ![Math $[f(t_1,\ldots,t_n)]$](/w/lib/exe/fetch.php?media=wiki:latex:/imgf0b91da75fd35f716439c2a2758299cf.png) if
if 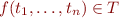 , and arbitrary otherwise
, and arbitrary otherwise
Implementing Congruence Closure
Congruence is an equivalence relation, so the algorithm is a special case of union-find algorithms for finding partitions.
We represent expressions as directed acyclic graphs, which are syntax trees for expressions, with sharing. This data structure is called E-graph.
Within this structure we have union of inverted trees, representing union-find data structure.
Inverted tree representing equivalence classes.
Example: Let 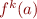 denote
denote 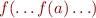 with
with  -fold application of
-fold application of  . Consider
. Consider
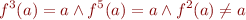
Apply the congruence closure algorithm to check its satisfiability.