This is an old revision of the document!
Sets and Relations
Sets
Sets are unordered collection of elements.
We denote a finite set containing only elements  ,
,  and
and  by
by 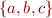 . The order and number of occurrences does not matter:
. The order and number of occurrences does not matter:
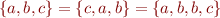 .
.
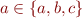
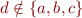 iff
iff 
Empty set:  . For every
. For every  we have
we have 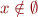 .
.
To denote large or infinite sets we can use set comprehensions: 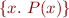 is set of all objects with property
is set of all objects with property  .
\[
.
\[
y \in \{ x. P(x) \} \ \leftrightarrow\ P(y)
\]
Notation for set comprehension: 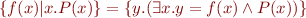
Sometimes the binder  can be inferred from context so we write simply
can be inferred from context so we write simply 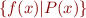 . In general there is ambiguity in which variables are bound. (Example: what does the
. In general there is ambiguity in which variables are bound. (Example: what does the  in
in  refer to in the expression:
\[
refer to in the expression:
\[
\{a \} \cup \{ f(a,b) \mid P(a,b) \}
\]
does it refer to the outerone  as in
as in  or is it a newly bound variable? The notation with dot and bar resolves this ambiguity.
or is it a newly bound variable? The notation with dot and bar resolves this ambiguity.
Subset:  means
means 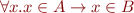
\[
A \cup B = \{ x. x \in A \lor x \in B \}
\] \[
A \cap B = \{ x. x \in A \land x \in B \}
\] \[
A \setminus B = \{ x. x \in A \land x \notin B \}
\]
Boolean algebra of subsets of some set  (we define
(we define 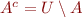 ):
):
 are associative, commutative, idempotent
are associative, commutative, idempotent- neutral and zero elements:
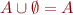 ,
, 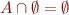
- absorption:
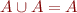 ,
, 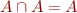
- deMorgan laws:
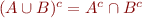 ,
, 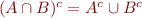
- complement as partition of universal set:
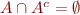 ,
, 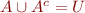
- double complement:
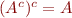
Which axioms are sufficient?
Infinte Unions and Intersections
Note that sets can be nested. Consider, for example, the following set  \[
\[
S = \{ \{ p, \{q, r\} \}, r \}
\]
This set has two elements. The first element is another set. We have 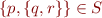 . Note that it is not the case that
. Note that it is not the case that
Suppose that we have a set  that contains other sets. We define union of the sets contained in
that contains other sets. We define union of the sets contained in  as follows:
\[
as follows:
\[
\bigcup B = \{ x.\ \exists a. a \in B \land x \in a \}
\] As a special case, we have \[
\bigcup \{ a_1, a_2, a_3 \} = a_1 \cup a_2 \cup a_3
\]
Often the elements of the set  are computed by a set comprehension of the form
are computed by a set comprehension of the form 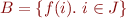 .
We then write
\[
.
We then write
\[
\bigcup_{i \in J} f(i)
\] and the meaning is \[
\bigcup \{ f(i).\ i \in J \}
\]
Therefore, 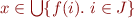 is equivalent to
is equivalent to  .
.
We analogously define intersection of elements in the set: \[
\bigcap B = \{ x. \forall a. a \in B \rightarrow x \in a \}
\] As a special case, we have \[
\bigcap \{ a_1, a_2, a_3 \} = a_1 \cap a_2 \cap a_3
\] We similarly define intersection of an infinite family \[
\bigcap_{i \in J} f(i)
\] and the meaning is \[
\bigcap \{ f(i).\ i \in J \}
\]
Therefore, 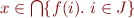 is equivalent to
is equivalent to  .
.
Relations
Pairs: \[
(a,b) = (u,v) \iff (a = u \land b = v)
\] Cartesian product: \[
A \times B = \{ (x,y) \mid x \in A \land y \in B \}
\]
Relations  is simply a subset of
is simply a subset of  , that is
, that is 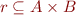 .
.
Note: \[
A \times (B \cap C) = (A \times B) \cap (A \times C)
\] \[
A \times (B \cup C) = (A \times B) \cup (A \times C)
\]
Diagonal relation
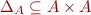 , is given by
\[
, is given by
\[
\Delta_A = \{(x,x) \mid x \in A\}
\]
Set operations
Relations are sets of pairs, so operations 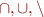 apply.
apply.
Relation Inverse
\[
r^{-1} = \{(y,x) \mid (x,y) \in r \}
\]
Relation Composition
\[
r_1 \circ r_2 = \{ (x,z) \mid \exists y. (x,y) \in r_1 \land (y,z) \in r_2\}
\]
Note: relations on a set  together with relation composition and
together with relation composition and  form a monoid structure:
\[
\begin{array}{l}
form a monoid structure:
\[
\begin{array}{l}
r_1 \circ (r_2 \circ r_3) = (r_1 \circ r_2) \circ r_3 \\ r \circ \Delta_A = r = \Delta_A \circ r
\end{array} \]
Moreover, \[
\emptyset \circ r = \emptyset = r \circ \emptyset
\] \[
r_1 \subseteq r_2 \rightarrow r_1 \circ s \subseteq r_2 \circ s
\] \[
r_1 \subseteq r_2 \rightarrow s \circ r_1 \subseteq s \circ r_2
\]
Relation Image
When  and
and 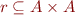 we define image of a set
we define image of a set  under relation
under relation  as
\[
as
\[
S\bullet r = \{ y.\ \exists x. x \in S \land (x,y) \in r \}
\]
Transitive Closure
Iterated composition let 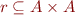 .
\[
\begin{array}{l}
.
\[
\begin{array}{l}
r^0 = \Delta_A \\
r^{n+1} = r \circ r^n
\end{array}
\]
So,  is n-fold composition of relation with itself.
is n-fold composition of relation with itself.
Transitive closure: \[
r^* = \bigcup_{n \geq 0} r^n
\]
Equivalent statement: 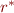 is equal to the least relation
is equal to the least relation  (with respect to
(with respect to  ) that satisfies
\[
) that satisfies
\[
\Delta_A\ \cup\ (s \circ r)\ \subseteq\ s
\]
or, equivalently, the least relation  (with respect to
(with respect to  ) that satisfies
\[
) that satisfies
\[
\Delta_A\ \cup\ (r \circ s)\ \subseteq\ s
\]
or, equivalently, the least relation  (with respect to
(with respect to  ) that satisfies
\[
) that satisfies
\[
\Delta_A\ \cup\ (s \circ s)\ \subseteq\ s
\]
Some Laws in Algebra of Relations
\[
(r_1 \circ r_2)^{-1} = r_2^{-1} \circ r_1^{-1}
\] \[
r_1 \circ (r_2 \cup r_3) = (r_1 \circ r_2) \cup (r_1 \circ r_3)
\] \[
(r^{-1})^{*} = (r^{*})^{-1}
\]
Binary relation 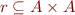 can be represented as a directed graph
can be represented as a directed graph 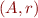 with nodes
with nodes  and edges
and edges 
- Graphical representation of
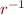 ,
, 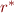 , and
, and 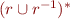
Equivalence relation  is relation with these properties:
is relation with these properties:
- reflexive:
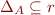
- symmetric:

- transitive:

Equivalence classes are defined by \[
x/r = \{y \mid (x,y) \in r
\]
The set  is a partition:
is a partition:
- each set non-empty
- sets are disjoint
- their union is

Conversely: each collection of sets  that is a partition defines equivalence class by
\[
that is a partition defines equivalence class by
\[
r = \{ (x,y) \mid \exists c \in P. x \in c \land y \in c \}
\]
Congruence: equivalence that agrees with some set of operations.
Partial orders:
- reflexive
- antisymmetric:
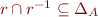
- transitive
Functions
Example: an example function 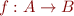 for
for 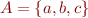 ,
, 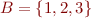 is
\[
is
\[
f = \{ (a,3), (b,2), (c,3) \}
\]
Definition of function, injectivity, surjectivity.
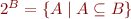
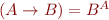 - the set of all functions from
- the set of all functions from  to
to  . For
. For  it is a strictly bigger set than
it is a strictly bigger set than  .
.
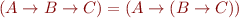 (think of exponentiation on numbers)
(think of exponentiation on numbers)
Note that  is isomorphic to
is isomorphic to 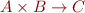 , they are two ways of representing functions with two arguments.
, they are two ways of representing functions with two arguments. 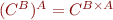
There is also isomorphism between
- n-tuples
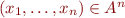 and
and - functions
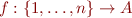 , where
, where 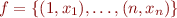
Function update
Function update operator takes a function 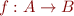 and two values
and two values  ,
,  and creates a new function
and creates a new function ![Math $f[a_0 \mapsto b_0]$](/w/lib/exe/fetch.php?media=wiki:latex:/imgcac49089d0ce3df1d660788d24f4ca1e.png) that behaves like
that behaves like  in all points except at
in all points except at  , where it has value
, where it has value  . Formally,
\[
f[a_0 \mapsto b_0](x) = \left\{\begin{array}{l}
. Formally,
\[
f[a_0 \mapsto b_0](x) = \left\{\begin{array}{l}
b_0, \mbox{ if } x=a_0 \\
f(x), \mbox{ if } x \neq a_0
\]
Domain and Range of Relations and Functions
For relation 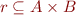 we define domain and range of
we define domain and range of  :
\[
:
\[
dom(r) = \{ x.\ \exists y. (x,y) \in r \}
\] \[
ran(r) = \{ y.\ \exists x. (x,y) \in r \}
\]
Clearly, 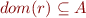 and
and 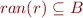 .
.
Partial Function
Notation: 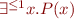 means
means 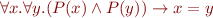 .
.
Partial function 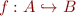 is relation
is relation 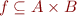 such that
\[
such that
\[
\forall x \in A. \exists^{\le 1} y.\ (x,y)\in f
\]
Generalization of function update is override of partial functions, 
More Properties
\[
S \bullet r = ran(\Delta_S \circ r)
\] \[
(S \bullet r_1) \bullet r_2 = S \bullet (r_1 \circ r_2)
\]
Further references
- Gallier Logic Book, Chapter 2