LARA

Set Constraints for Algebraic Datatype Inference

We want that our compiler detects correctly the possible subset of types for each function.

Example

Consider data type definition 

type form = Atom of string
          | And of form * form
          | Or of form * form
          | Not of form

We represent values of this data type as ground terms in language 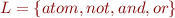$L = \{ atom,not,and,or\}$.

Define function: 

let rec elimOr(f : form) : form =
    match f with
 S1: | Atom s -> Atom s
 S2: | And(f1,f2) -> And(elimOr f1, elimOr f2)
 S3: | Or(f1,f2) -> Not(And(Not(elimOr f1), Not(elimOr f2)))
 S4: | Not(f1) -> Not(elimOr f1)

We infer the subset of formulas returned by this function using set constraints. Introduce set for each case of pattern matching expression. Let 'res' denote the set of values that can be returned by the function. We obtain the system of constraints:

\begin{equation*} \begin{array}{l} atom \subseteq S_1 \\ and(res, res) \subseteq S_2 \\ not(and(not(res), not(res))) \subseteq S_3 \\ not(res) \subseteq S_4 \\ res = S_1 \cup S_2 \cup S_3 \cup S_4 \end{array} \end{equation*}

We can prove that the least fixpoint is the same as the least fixpoint of

\begin{equation*} res = atom \cup and(res,res) \cup not(res) \end{equation*}

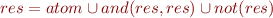
the last expression is a description of the solution set. We can use it later on to prove that the result does not mention 'or' syntax tree node.