Quantifier Instantiation

Quantifier instantiation:

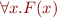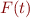given a conjunct $\forall x.F(x)$ and a term $t$ occurring in other conjuncts, generate $F(t)$ and continue
in general this is incomplete
it cannot be complete because quantified combination of linear arithmetic with uninterpreted functions symbols is highly undecidable

Triggers: instantiate e.g. 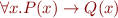$\forall x. P(x) \rightarrow Q(x)$ only if you find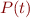 $P(t)$

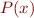$P(x)$ acts as a guard to limit instantiations
introduced in Simplify: a theorem prover for program checking
user-defined trigger terms: specify terms whose instances, if present in the ground part of the formula, will lead to instantiation
for more information see PhD Thesis of Michal Moskal

Traditionally resolution-based provers have more sophisticated quantifier handling (but have no decision procedures). This is changing and both approaches integrate techniques from others.

Solving Quantified Verification Conditions using Satisfiability Modulo Theories
Efficient E-matching for SMT solvers by Leonardo de Moura and Nikolaj Bjørner

Some approaches combine DPLL(T) solvers and resolution-based solvers

SPASS+T by Virgile Prevosto and Uwe Waldmann