Quantifier Elimination from Conjunction of Literals is Sufficient

¹⁾To show constructively that a theory has quantifier elimination, it suffices to show that we can eliminate an existential quantifier applied to a conjunction of literals, that is, show that each formula of the form:

$\begin{equation*} \exists x. \bigwedge_{i=1}^n L_i \end{equation*}$

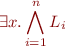
where each 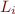$L_i$ is a literal, is equivalent to a quantifier-free formula. Indeed, suppose we know how to eliminate quantifiers from conjunctions of formulae, then if $F$ is a quantifier-free formula, we can write it in disjunctive normal form

$\begin{equation*} \bigvee_{j=1}^m \bigwedge_{i=1}^n L_{ij} \end{equation*}$

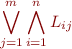
and use the fact that

$\begin{equation*} \exists x. \bigvee_{j=1}^m \bigwedge_{i=1}^n L_{ij} \end{equation*}$

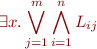
is equivalent to

$\begin{equation*} \bigvee_{j=1}^m \exists x. \bigwedge_{i=1}^n L_{ij} \end{equation*}$

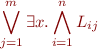
Finally, to eliminate a universal quantifier

$\begin{equation*} \forall x. F \end{equation*}$

where $F$ is quantifier-free, we transform $\lnot F$ into disjunctive normal form, and use the fact that $\forall x. F$ is equivalent to $\lnot \exists x. \lnot F.$

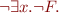
¹⁾

taken from Quantifier Elimination to which it was originally contributed, so the Wikipedia sharing rights apply