Proof Theory for Propositional Logic

Notion of a proof system

A set of proof rules, each of which specifies how to derive a formula from zero or more other formulas.

Typical requirement: polynomial-time algorithm to check whether a rule application is valid according to the rule system

We write 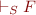$\vdash_S F$ if we can derive formula in some proof system $S$ . We omit $S$ when it is clear.

Proof tree and proof sequences.

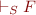Proof complexity: given $F$ such that $\vdash_S F$ , the size of smallest proof of $F$ in $S$ .

System $S$ is sound if for every formula $F$ ,

$\begin{equation*} (\vdash_S F) \rightarrow (\models F) \end{equation*}$

We can only prove true formulas.

System $S$ is complete if for every formula $F$ ,

$\begin{equation*} (\models F) \rightarrow (\vdash F) \end{equation*}$

We can prove all valid formulas.

A simple A sound and complete proof system.

Rule 1: Case analysis rule:

$\begin{equation*} \frac{P\{p \mapsto {\it true}\}\ ;\ P\{p \mapsto {\it false}\}} {P} \end{equation*}$

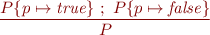
Rule 2: Evaluation rule: derive $P$ if $P$ has no variables and it evaluates to true.

We can also add simplification rules. Adding sound rules preserves soundness and completeness.

Recall Gentzen's proof system from proofs and induction part of lecture02, ignoring rules for predicates and induction.