Proving Correctness of Recursive Multiplication
We prove that this function computes x*y:
private static int f(int x, int y)
{
if (y == 0) {
return 0;
} else {
if (y % 2 == 0) {
int z = f(x, y / 2);
return (2 * z);
} else {
return (x + f(x, y - 1));
}
}
}
By translating Java code into math, we obtain the following mathematical definition of  :
:
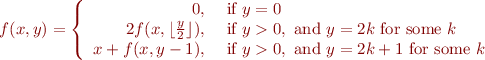
By induction on  we then prove
we then prove 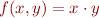 .
.
- Base case. Let
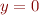 . Then
. Then 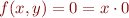
- Inductive hypothesis. Assume that the claim holds for all values less than
 .
. - Goal: show that it holds for
 where
where  .
. - Case 1:
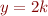 . Note
. Note  . By definition and I.H.
. By definition and I.H.
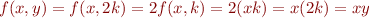
-
- Case 2:
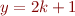 . Note
. Note 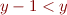 . By definition and I.H.
. By definition and I.H.
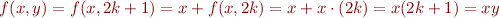
This completes the proof.