LARA

Pointer Analyses

Analyses with graph-based models of memory

This summary was compiled from the lecture notes and from reference 1 below (where the graph, its construction and other details are explained much more precisely).

The idea here is to represent the state of the memory after some statement in the program by building a graph. A node in the graph represents either

  • a simple variable (then called a variable node) or
  • a set of heap nodes $new_i$ (recall from preivous section that $new_i$ is the set of all objects allocated on the heap at program point $i$)

Variable nodes and fields of heap nodes model locations in run-time data structures where pointers may be stored.

Edges in the graph represent pointer values. Edges originate either from variable nodes or from fields within heap nodes and are directed towards heap nodes. (Note: variable nodes do not contain fields, therefore edges cannot be directed towards variable nodes).

The graph contains a finite number of nodes if we build one abstract location $new_i$ per allocation site $i$. This allocation site model was the one presented in class, although there could be other methods for merging heap nodes in the graph.

Loops represent the unbounded size of a data structure.

Assignments

We consider assignments of the form y = x.f or x.f = y. These change the graph in the following way:

  • y = x.f

Add an edge directed from the variable node for y to the set of nodes reached by leaving fields in x (or the set of nodes that x belongs to). This is the green edge in the diagram below. Remove the old outgoing edge of y (the red edge in the diagram below). This is called a strong update because we are replacing the old edge with a new edge. If we added the new edge without removing the old one, then we would be performing a weak update.

  • x.f = y

Add an edge from fields in the set of x to the set of nodes that y points to. This is the green edge in the diagram below. This is a weak update since we do not remove old edges leaving the fields of the nodes in x (or the set of nodes, denoted 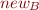$new_B$, which includes the object that x points to). If we were sure that 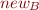$new_B$ contains a single heap node (and thus that the variable node x points to a single object), then we could remove the old edge, and have a strong update.

We want to do strong updates as much as possible because they are the ones that give us more information about what is going on in the memory (who is pointing to who). Therefore we could split abtract locations into smaller sets if they enable us to do a strong update, and then can merge them later if possible.

References

  1. Analysis of pointers and structures
  2. Detecting conflicts between structure accesses

Steensgard's analysis

A nonstandard type system: each type describes a set of locations (static, stack, and dynamically allocated).

  • flow insensitive
  • interprocedural
  • almost linear - unification based

Example: x has type 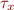$\tau_x$ and y has type 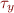$\tau_y$. If there is a statement x=y and y can store a pointer, then types of x and y are unified i.e.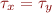 $\tau_x = \tau_y$

Unification:

Start optimistically by saying all variables have distinct types, and then merge types when there is an assignment. In other words, we are computing the smallest equivalence relation. For this purpose, we can use a union-find data structure (inverted trees) to represent equivalence classes.

References

Andersen's analysis

Here, when there is an assignment of the form x=y, we say that the type of y is a subset of the type of x i.e. 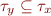$\tau_y \subseteq \tau_x$ which is the same as $\forall l. l \in \tau_y \rightarrow l \in \tau_x$.

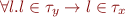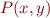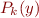Context is program specialization: given program $P(x,y)$ and a known input $k$, generate a specialized, more efficient, program $P_k(y)$ such that $P_k(y) = P(k,y)$.

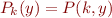Used in run-time specialization.

Needed a series of analyses, but most known for its pointer analysis.

  • context sensitive
  • subset based (as opposed to unification-based)

References

Further References

Context-sensitive interprocedural pointer analyses: