This is an old revision of the document!
Playground
Problem 1: Linear Extension
Let 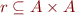 be an arbitrary relation and
be an arbitrary relation and  a partial order on
a partial order on  .
.
a) Assume 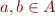 to be incomparable:
to be incomparable: 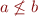 and
and 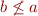 . Show that the transitive closure of the relation
. Show that the transitive closure of the relation  is a partial order on
is a partial order on  .
.
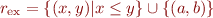
b) Use (a) to show if  is finite then every order
is finite then every order  on
on  has a linear extension.
A total order
has a linear extension.
A total order  is a linear extension of a partial order
is a linear extension of a partial order  if, whenever
if, whenever  implies that
implies that  .
.
c) Use (a) to show there is a finite number of total orders  such that for all
such that for all 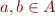 we have
we have
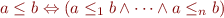
d) Show that  is a linear extension of
is a linear extension of  if and only if
if and only if 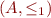 is a total order and the identity function is a monotone function from
is a total order and the identity function is a monotone function from 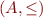 to
to 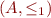 .
.
Perl
- Write a regular expression that matches a pair of <d> and </d> XML tags and the text between them. The text between the tags can include any other tags.
- The lexical analyzer typically finds the longest matches. Some languages such as Perl have introduced laziness in matching. By adding a question mark to the end of an operator its lazy version is obtained. For example, given an input 'aaaaa', the expression
 will match the entire input. But the lazy version
will match the entire input. But the lazy version  matches the minimum number of possible characters, which is the empty string. Using lazy repetition find a compact representation for the first part.
matches the minimum number of possible characters, which is the empty string. Using lazy repetition find a compact representation for the first part.