Playground
Problem 1: Linear Extension
Let 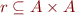 be an arbitrary relation and
be an arbitrary relation and  a partial order on
a partial order on  .
.
a) Assume 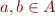 to be incomparable:
to be incomparable: 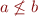 and
and 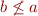 . Show that the transitive closure of the relation
. Show that the transitive closure of the relation  is a partial order on
is a partial order on  .
.
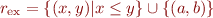
b) Use (a) to show if  is finite then every order
is finite then every order  on
on  has a linear extension.
A total order
has a linear extension.
A total order  is a linear extension of a partial order
is a linear extension of a partial order  if, whenever
if, whenever  implies that
implies that  .
.
c) Use (a) to show there is a finite number of total orders  such that for all
such that for all 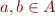 we have
we have
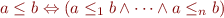
d) Show that  is a linear extension of
is a linear extension of  if and only if
if and only if 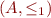 is a total order and the identity function is a monotone function from
is a total order and the identity function is a monotone function from 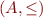 to
to 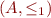 .
.