This is an old revision of the document!

Non-Ground Instantiation and Resolution

Non-Ground Resolution

Why apply resolution only on ground terms? Consider arbitrary clauses $C, D$ and any atom $A$ . \[ \frac{C \cup \{\lnot A\}\ \ \ D \cup \{A\}}

   {C \cup D}

Is this non-ground resolution rule sound?

\[ \frac{(\forall \vec x.\ (\lnot C) \rightarrow \lnot A)\ \ \ (\forall \vec x. (\lnot A) \rightarrow D)}

   {\forall \vec x.\ \lnot C \rightarrow D}

Non-Ground Instantiation

For arbitrary substitution: \[ \frac{C}{subst(\sigma)(C)} \]

Is this non-ground instantiation rule sound?

Illustration of rules.

Reducing the Search Space

More powerful rules.

But more choices at each step.

If we try to do the proof, how do we know what to instantiate with? we instantiate to enable subsequent resolution rule.

Resolution with instantiation \[ \frac{C \cup \{\lnot A_1\}\ \ \ D \cup \{A_2\}}

   {subst(\sigma_1)(C) \cup subst(\sigma_2)(D)}

\] such that 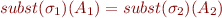$subst(\sigma_1)(A_1) = subst(\sigma_2)(A_2)$ .

Resolution with instantiation generalizes resolution and ground resolution.

One complete proof system contains:

instantiation
resolution with instantiation

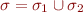Note: if we apply instantiation that renames variables in each clause, then $\sigma_1$ and $\sigma_2$ can have disjoint domains and we let $\sigma = \sigma_1 \cup \sigma_2$ , obtaining

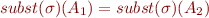Note: $\sigma$ such that $subst(\sigma)(A_1) = subst(\sigma)(A_2)$ is called a unifier for $\{A_1,A_2\}$ .

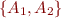Further step: do we need to consider all unifiers?

Most general unifier. To compute it we can use the standard Unification algorithm.