Logic and Automata - Introduction

Satisfiability of $F$ : is there an interpretation in which $F$ is true.

Validity of $F$ : is $F$ true in all interpretations (reduces to satisfiability of $\lnot F$ ).

Some techniques for establishing this for quantified formulas:

quantifier elimination (seen before)
automata-based techniques - this lecture and next one
game-based techniques (perhaps next week)

Common for quantifier elimination and automata-based techniques: characterize the set of all models (interpretations in which $F$ is true).

More generally, for each formula with free variables, we compute the relation that the formula defines.

Example

Compute the unary relation (set) corresponding to this formula $F(z)$ :

$\begin{equation*} \exists x. \exists y.\ z = 2 x + 1 \land z = 3 y + 2 \end{equation*}$

Basic Idea

We come up with a 'nice' representation of relations

in quantifier elimination these are particular quantifier-free formulas
in automata-based methods that we will look at, we represent relations as regular languages

In Lecture15 we have seen that Presburger arithmetic is decidable using quantifier elimination.

Today we see an alternative decision method, based on Presburger arithmetic, and then generalize it to more expressive logics: monadic second-order logic over strings and trees.
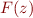
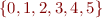