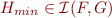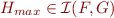This is an old revision of the document!
Interpolation for Propositional Logic
Definition of Interpolant:
Given two propositional formulas  and
and  , an interpolant for
, an interpolant for 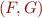 is a propositional formula
is a propositional formula  such that:
such that:
1) 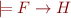
2) 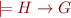
3) 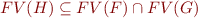
Note that  by transitivity of
by transitivity of  . The interpolant extracts the essential part of formula
. The interpolant extracts the essential part of formula  which makes
which makes  imply
imply  .
.
Let  denote the operator that eliminates propositional quantifiers (see QBF and Quantifier Elimination).
denote the operator that eliminates propositional quantifiers (see QBF and Quantifier Elimination).
Here are two simple ways to construct an interpolant:
- We can quantify existentially all variables in
 that are not in
that are not in  .
.
 where
where 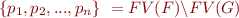
- We can quantify universally all variables in
 that are not in
that are not in  .
.
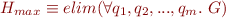 where
where 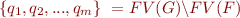
Definition: 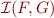 denote the set of all interpolants for
denote the set of all interpolants for 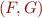 , that is,
\[
, that is,
\[
{\cal I}(F,G) = \{ H \mid H \mbox{ is interpolant for $(F,G)$ \}
\]
Theorem: The following properties hold for  ,
,  ,
, 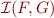 defined above:
defined above:
We can also derive interpolants from resolution proofs, as we will see in lecture07.
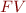 denotes the set of free variables in the given propositional formula, see
denotes the set of free variables in the given propositional formula, see