Interpolants from Resolution Proofs
Interpolants in resolution: instead of validity of implication, we look at unsatisfiability.
Let  ,
,  be sets of clauses such that
be sets of clauses such that 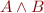 is not satisfiable. An interpolant is a formula
is not satisfiable. An interpolant is a formula  such that
such that
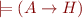 and
and 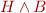 is not satisfiable and
is not satisfiable and 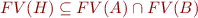
Construct resolution tree that derives a contradiction from  . The tree has elements of
. The tree has elements of  as leaves and results of application of resolution as nodes. For each clause
as leaves and results of application of resolution as nodes. For each clause  in resolution tree we define recursively formula
in resolution tree we define recursively formula  and show that
and show that  is interpolant for these two formulas:
is interpolant for these two formulas:
where  denotes the conjunction of those literals from
denotes the conjunction of those literals from  whose propositional variables belong to
whose propositional variables belong to 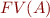 , similarly for
, similarly for  .
.
It follows that for empty clause the 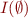 is the interpolant for
is the interpolant for 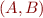 .
.
Construction of  :
:
- if
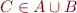 then
then- if
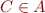 then
then 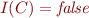
- if
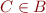 then
then 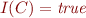
- if
 is result of applying resolution to
is result of applying resolution to  ,
,  along propositional variable
along propositional variable  where
where  , and
, and 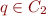 , then
, then- if
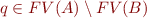 then
then 
- if
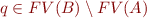 then
then 
- if
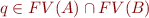 then
then 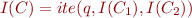
We prove that  has the desired property by induction on the structure of the resolution proof tree.
has the desired property by induction on the structure of the resolution proof tree.
More information in e.g.

