Ground Instantiation plus Ground Resolution as a Proof System
We introduce this proof system as an intermediate step between the naive enumeration algorithm based on Herbrand's theorem and resolution for first-order logic.
Our goal is to avoid explicit enumeration and apply proof system where we do as little search (guessing) as possible, while still being complete.
Definition
The proof system has two rules: ground instantiation and ground resolution.
Ground Instantiation Rule
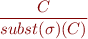
where  is a clause and
is a clause and  is a ground substitution.
is a ground substitution.
Ground substitution is of the form 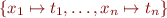 where each
where each  is a ground term.
is a ground term.
Ground Resolution Rule
If  is a ground atom and
is a ground atom and  are ground claues, then
are ground claues, then
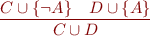
Note that this is propositional resolution where propositional variables have “long names” (they are ground atoms).
Example
Completeness
The proof is based on Herbrand's Expansion Theorem (see also the proof of Compactness for First-Order Logic).
Suppose a set  of clauses is contradictory. By Herbrand's Expansion Theorem and Compactness Theorem for Propositional Formulas, some finite subset
of clauses is contradictory. By Herbrand's Expansion Theorem and Compactness Theorem for Propositional Formulas, some finite subset 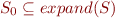 is contradictory. Then there exists a derivation of empty clause from
is contradictory. Then there exists a derivation of empty clause from 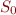 viewed as set of propositional formulas, using propositional resolution. In other words, there exists a derivation of empty clause from
viewed as set of propositional formulas, using propositional resolution. In other words, there exists a derivation of empty clause from 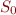 using ground resolution rule. Each element of
using ground resolution rule. Each element of 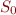 can be obtained from an element of
can be obtained from an element of  using instantiation rule. This means that there exists a proof tree whose leaves are followed by a single application of instantiation rule, and inner nodes contain ground resolution steps.
using instantiation rule. This means that there exists a proof tree whose leaves are followed by a single application of instantiation rule, and inner nodes contain ground resolution steps.