Homework 09 - Due Wednesday, April 30

Problem 1

Describe current progress on your project.

Problem 2

Prove that the quantifier-free theory of term algebras is convex (See Calculus of Computation Textbook, Section 10.3.1). That is, show that, if $C$ is a conjunction of literals of form $t=t'$ and $t\neq t'$ where $t,t'$ are terms in some language (containing variables), and if formula

$\begin{equation*} C \rightarrow \bigvee_{i=1}^n t_i=t'_i \end{equation*}$

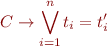
is valid (holds for all values of variables) in the Herbrand interpretation (where elements are ground terms and 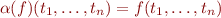$\alpha(f)(t_1,\ldots,t_n)=f(t_1,\ldots,t_n)$ ), then for some $i$

$\begin{equation*} C \rightarrow t_i=t'_i \end{equation*}$

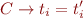
holds for all values of variables in the Herbrand interpretation.

If you use in your solution any theorem about term algebras that we did not prove in the class, you need to prove the theorem as well.