Fixpoints
Definition: Given a set  and a function
and a function 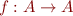 we say that
we say that  is a fixed point (fixpoint) of
is a fixed point (fixpoint) of  if
if 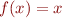 .
.
Definition: Let 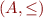 be a partial order, let
be a partial order, let 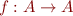 be a monotonic function on
be a monotonic function on 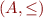 , and let the set of its fixpoints be
, and let the set of its fixpoints be 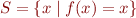 . If the least element of
. If the least element of  exists, it is called the least fixpoint, if the greatest element of
exists, it is called the least fixpoint, if the greatest element of  exists, it is called the greatest fixpoint.
exists, it is called the greatest fixpoint.
Note:
- a function can have various number of fixpoints. Take
 ,
, 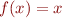 the set of fixedpoints is
the set of fixedpoints is 
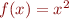 the set of fixedpoints is
the set of fixedpoints is 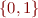
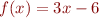 has exactly one fixpoint:
has exactly one fixpoint: 
- a function can have at most one least and at most one greatest fixpoint
We can use fixpoints to give meaning to recursive and iterative definitions
- key to describing arbitrary long executions in programs