Fixed-Width Bitvectors
Bitvector: integer from some finite inteval of length 
Example: ![Math $[0,2^{32}-1]$](/w/lib/exe/fetch.php?media=wiki:latex:/img40765ecd83321da9aa339ef14fc3f463.png)
Logic on bitvectors.
- formulas for +.
We can reduce reasoning on bitvectors to reasoning in propositional logic.
Application:
- exact reasoning about Java integers
- finding counterexamples for formulas over unbounded integers
Expressing Linear Arithmetic with Given Bounds
Consider formulas in our linear arithmetic language:
T ::= K | V | (T + T) | (T - T) | (K * T) | (T / K) | (T % K) F ::= (T=T) | (T < T) | (T > T) | (~F) | (F & F) | (F|F) V ::= x | y | z | ... K ::= 0 | 1 | 2 | ...
Suppose we are given bounds for all integer variables and that they belong to ![Math $[0,2^B-1]$](/w/lib/exe/fetch.php?media=wiki:latex:/imga696b7d7279fe30312a8ece852827e2f.png) .
.
We present translation from  to equisatisfiable
to equisatisfiable 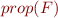 in propositional logic. That is,
in propositional logic. That is,
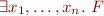
is equivalent to

Where 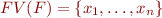 and
and 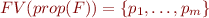 .
.
For each bounded integer variable ![Math $x \in [0,2^B-1]$](/w/lib/exe/fetch.php?media=wiki:latex:/img5bfc05cbab5e68487065c2f198dbff78.png) we introduce propositional variables corresponding to its binary representation.
we introduce propositional variables corresponding to its binary representation.
The constructions for operations correspond to implementing these operations in hardware circuits:
- adder for +
- shift for *
- comparator for <, =
Example: propositional formula expressing 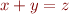 when
when ![Math $x,y,z \in [0,2^B-1]$](/w/lib/exe/fetch.php?media=wiki:latex:/img7fe32acb1f192dbb87a550dbd2d16f80.png) .
.
Note that subtraction can be expressed using addition, similarly for / and %.
How to express inverse operations for nested terms?
Additional pre-processing is useful. Much more on such encodings we will see later, and can also be found here:
Later we will see how to prove that linear arithmetic holds for all bounds and not just given one.