Finite Models Imply Decidability
Now for some positive results.
Theorem: Suppose that  is a subset of all first-order logic sentences such that for all
is a subset of all first-order logic sentences such that for all 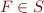 ,
,
 , and
, and- if
 has a model, then
has a model, then  has a finite model
has a finite model
Then there exists an algorithm that, given a formula from 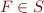 , determinies whether
, determinies whether  is valid.
is valid.
Note: such algorithm is called a decision procedure for the class of formulas  .
.
Note: we have just shown that such algorithm does not exists for the set of all sentences in first-order logic. There is only an algorithm (e.g. resolution) that will terminate when formula is valid, but need not terminate on invalid formulas.
Proof:
Prover and counterexample finder running in parallel.