Formulas with only Finite Models but Infinite Set of Ground Terms

Example:

$\begin{equation*} P(a) \land (\forall x.\ P(x) \rightarrow \lnot P(f(x))) \land (\forall x. x=a \lor x=b) \end{equation*}$

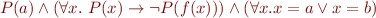
Is this formula satisfiable? yes

What are possible cardinalities for models? they all have exactly two elements.

What are ground terms for this formula?

Cardinality is infinite!

By Herbrand theorem, does every satisfiable first-order logic formula have Herbrand model? Only if formula has no equality! We made this assumption when proving Herbrand theorem.