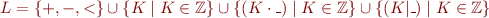Definition of Presburger Arithmetic
Minimalistic Language of Presburger Arithmetic
Consider 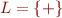 and consider as
and consider as  the set of all interpretations with domain
the set of all interpretations with domain 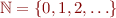 where
where  is interpreted as addition of natural numbers (these interpretations differ only in values for free variables. This is one definition of Presburger arithmetic over natural numbers.
is interpreted as addition of natural numbers (these interpretations differ only in values for free variables. This is one definition of Presburger arithmetic over natural numbers.
This theory is very simple to describe, but it is very far from allowing quantifier-elimination. For example, it does not have a name for zero, so we cannot express  . It also does not have a way to express
. It also does not have a way to express  .
.
Language of Presburger Arithmetic that Admits QE
We look at the theory of integers with addition.
- introduce constant for each integer constant
- introduce not only addition but also subtraction
- to conveniently express certain expressions, introduce function
 for each
for each  , to be interpreted as multiplication by a constant,
, to be interpreted as multiplication by a constant, 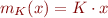 . We write
. We write  as
as 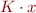
- to enable quantifier elimination from
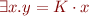 introduce for each
introduce for each  predicate
predicate 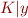 (divisibility by constant)
(divisibility by constant)
The resulting language