Deciding a Language of Sets (and Relations)

Consider a simple language of sets:

$\begin{equation*} \begin{array}{l} S ::= V \mid S \cup S \mid S \cap S \mid S \setminus S \mid \mathbf{U} \mid \emptyset \\ A ::= (S = S) \mid (S \subseteq S) \mid card(S){=}c \mid card(S) \leq c \mid card(S) \geq c \\ F ::= F \lor F \mid F \land F \mid \lnot F \mid A \\ c ::= 0 \mid 1 \mid 2 \mid ... \end{array} \end{equation*}$

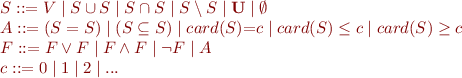
We show that this language is decidable by reduction to universal class.

While BAPA is more expressive with respect to cardinalities, the advantage of the present method is that it allows the use of certain relations.

Decision Procedures for Set-Valued Fields

However, see On Combining Theories with Shared Set Operations for a way to combine BAPA with logics that support relations.