This is an old revision of the document!
Compactness Theorem for Propositional Logic
Among the application of compactness theorem is showing that certain theorem proving methods are “complete in the limit”.
Notation:

 is the countably infinite set of all propositional variables of interest
is the countably infinite set of all propositional variables of interest- interpretation
 maps propositional variables
maps propositional variables  to truth values
to truth values 
- if
 is a propositional formula,
is a propositional formula,  means that
means that  is true when the variables are interpreted according to
is true when the variables are interpreted according to 
- if
 is a set of formulas,
is a set of formulas,  means: for each
means: for each 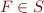 ,
, 
Theorem (Compactness Theorem for Propositional Logic): Let  be a (possibly infinite) set of propositional formulas. Then
be a (possibly infinite) set of propositional formulas. Then  is satisfiable if and only if every finite subset of
is satisfiable if and only if every finite subset of  is satisfiable.
is satisfiable.
Equivalent statement of compactness: If a set  is not satisfiable, then some finite subset of
is not satisfiable, then some finite subset of  is not satisfiable.
is not satisfiable.
If we allow infinite disjunctions in formulas, compactness fails. Note that we do not consider formulas with infinite connectives as propositional formulas (such formulas are usually called 'infinitary'), and from that reason the compactness theorem does not apply to this example.
Example. 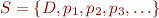 where
where 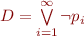 , that is,
, that is,  is equivalent to
is equivalent to 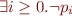 .
In this example, every finite subset of
.
In this example, every finite subset of  is satisfiable, but
is satisfiable, but  itself is not.
itself is not.
Proof of the compactness theorem: One direction is trivial: if  is satisfiable then there exists
is satisfiable then there exists  such that
such that  . Then for every finite subset
. Then for every finite subset  we have
we have 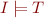 , so
, so  is satisfiable. We need to show the converse.
is satisfiable. We need to show the converse.
Intuition: A finitely satisfiable set has “all finite pieces” satisfiable (using potentially different interpretations). The question is whether we can somehow assemble interpretations for all finite pieces  into one large interpretation for the entire infinite set
into one large interpretation for the entire infinite set  . We will define such interpretation by extending it variable by variable, while preserving finite satisfiability for interepretations that begin with values for propositional variables chosen so far.
. We will define such interpretation by extending it variable by variable, while preserving finite satisfiability for interepretations that begin with values for propositional variables chosen so far.
Let  be finitely satisfiable. Let
be finitely satisfiable. Let 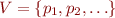 be the sequence of all propositional variables for formulas in
be the sequence of all propositional variables for formulas in  (this set is countable by our assumption on Propositional Logic Syntax, but can be infinite).
(this set is countable by our assumption on Propositional Logic Syntax, but can be infinite).
Given a sequence of boolean values  of length
of length  , by an
, by an 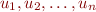 -interpretation we mean an interpretation
-interpretation we mean an interpretation  such that
such that 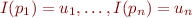 .
.
We will define interpretation 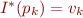 where the sequence of values
where the sequence of values 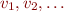 is given as follows:
\[
is given as follows:
\[
v_{k+1} = \left\{\begin{array}{l}
{\it false}, \mbox{ if for every finite } T \subseteq S, \mbox{ there exists a } v_1,\ldots,v_k,{\it false}-\mbox{interpretation } I \mbox{ such that } I \models T
{\it true}, \mbox{otherwise}
\]
We next show by induction the following.
Claim: For every non-negative integer  , every finite subset
, every finite subset  has a
has a 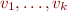 -interpretation
-interpretation  such that
such that 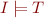 .
.
Base case: For  the statement reduces to claim that every finite subset of
the statement reduces to claim that every finite subset of  is satisfiable, which is an assumption of the theorem.
is satisfiable, which is an assumption of the theorem.
Inductive step: Assume the claim for  : every finite subset
: every finite subset  has a
has a 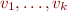 -interpretation
-interpretation  such that
such that 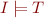 , we show that the statement holds for
, we show that the statement holds for  . If
. If 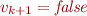 , the inductive statement holds by definition of
, the inductive statement holds by definition of  . Let
. Let 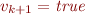 . Then by definition of
. Then by definition of  , there exists a finite set
, there exists a finite set  that has no
that has no 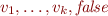 interpretation. We wish to show that every finite set
interpretation. We wish to show that every finite set  has a
has a 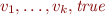 interpretation such that
interpretation such that  . Take any such set
. Take any such set  . Consider the set
. Consider the set  . This is a finite set, so by inductive hypothesis, it has a
. This is a finite set, so by inductive hypothesis, it has a 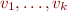 -interpretation
-interpretation  . Because
. Because 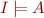 which has no
which has no 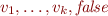 -interpretation, we have
-interpretation, we have 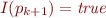 . Therefore,
. Therefore,  is a
is a 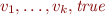 -interpretation for
-interpretation for  , and therefore for
, and therefore for  . This completes the inductive proof.
. This completes the inductive proof.
We finally show that  . Let
. Let 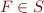 . Let
. Let 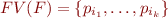 and
and 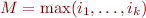 . Then
. Then 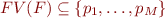 . The set
. The set  is finite, so, by the Claim, it has a
is finite, so, by the Claim, it has a  -interpretation
-interpretation  such that
such that  . Because
. Because 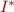 is also a
is also a  -interpretation, we have
-interpretation, we have  .
.
End of Proof.