This is an old revision of the document!
Chaotic Iteration in Abstract Interpretation
In Abstract Interpretation Recipe, note that if the set of program points is  , then we are solving the system of eqautions in
, then we are solving the system of eqautions in  variables
variables  \[
\begin{array}{l}
\[
\begin{array}{l}
g_1 = H_1(g_1,\ldots,g_n) \\ \ldots \\ g_i = H_i(g_1,\ldots,g_n) \\ \ldots \\ g_n = H_n(g_1,\ldots,g_n) \\
\end{array} \] where \[
H_i = g_i \sqcup \bigsqcup_{(p_j,p_i) \in E} sp^{\#}(g_j,r(p_j,p_i))
\]
The approach given in Abstract Interpretation Recipe computes in iteration  values
values 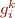 by applying all equations in parallel to previous values:
\[
\begin{array}{ll}
by applying all equations in parallel to previous values:
\[
\begin{array}{ll}
g^{k+1}_1 = H_1(g^k_1,\ldots,g^k_n) \\
\ldots \\
g^{k+1}_i = H_i(g^k_1,\ldots,g^k_n) & \mbox{\bf parallel iteration} \\
\ldots \\
g^{k+1}_n = H_n(g^k_1,\ldots,g^k_n) \\
\end{array} \]
What happens if we update values one-by-one? Say in one iteration we update  -th value, keeping the rest same:
\[
\begin{array}{ll}
-th value, keeping the rest same:
\[
\begin{array}{ll}
g^{k+1}_i = H_i(g^k_1,\ldots,g^k_n) \\
g^{k+1}_j = g^k_j, \mbox{ for } j \neq i & \mbox{\bf chaotic iteration}
\end{array}
\]
here we require that the new value 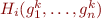 differs from the old one
differs from the old one 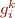 , otherwise we select a different one.
Then we pick a different
, otherwise we select a different one.
Then we pick a different  , as long as the result changes. This is chaotic iteration.
, as long as the result changes. This is chaotic iteration.
Questions:
- Does chaotic iteration converge if parallel converges?
- If it converges, will it converge to same value?
- If it converges, how many steps will convergence take?
- What is a good way of choosing index
 ?
?
Let  be vector of values
be vector of values  in parallel iteration and
in parallel iteration and  be vector of values in chaotic iteration, starting from the same initial lattice value
be vector of values in chaotic iteration, starting from the same initial lattice value 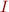 .
.
Compare values 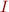 ,
, 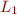 ,
,  ,
, 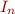 ,
,  in the lattice.
in the lattice.
References
- Principles of Program Analysis, Chapter 6