Chaotic Iteration in Abstract Interpretation: How to compute the fixpoint?
In Abstract Interpretation Recipe, note that if the set of program points is  , then we are solving the system of eqautions in
, then we are solving the system of eqautions in  variables
variables 
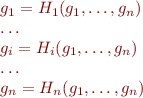
where
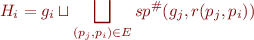
The approach given in Abstract Interpretation Recipe computes in iteration  values
values 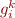 by applying all equations in parallel to previous values:
by applying all equations in parallel to previous values:
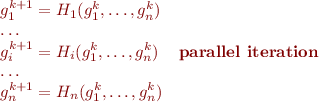
What happens if we update values one-by-one? Say in one iteration we update  -th value, keeping the rest same:
-th value, keeping the rest same:
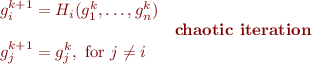
here we require that the new value 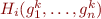 differs from the old one
differs from the old one 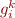 . An iteration where at each step we select some equation
. An iteration where at each step we select some equation  (arbitrarily) is called chaotic iteration. It is abstract representation of different iteration strategies.
(arbitrarily) is called chaotic iteration. It is abstract representation of different iteration strategies.
Questions:
- Does chaotic iteration converge if parallel converges?
- If it converges, will it converge to same value?
- If it converges, how many steps will convergence take?
- What is a good way of choosing index
 (iteration strategy), example: take some permutation of equations
(iteration strategy), example: take some permutation of equations
 be vectors of values
be vectors of values  in parallel iteration and
in parallel iteration and
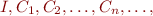 be vectors of values
be vectors of values  in chaotic iteration
in chaotic iteration
(starting from the same initial lattice value  )
)
Compare values  ,
, 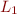 ,
,  ,
, 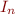 ,
,  in the lattice
in the lattice
Worklist Algorithm and Iteration Strategies
Observation: in practice 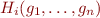 depends only on small number of
depends only on small number of 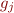 , namely predecessors of node
, namely predecessors of node 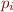
Consequence: if we chose  , next time it suffices to look at successors of
, next time it suffices to look at successors of  (saves traversing CFG)
(saves traversing CFG)
This leads to a worklist algorithm:
- initialize lattice, put all equations in worklist
- choose
 , find new
, find new  , remove
, remove  from worklist
from worklist - if
 has changed, update it and add to worklist
has changed, update it and add to worklist 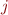 for
for  successor of
successor of 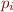
Algorithm terminates when worklist is empty (no more changes)
Useful iteration strategy: reverse postorder and strongly connected components
Reverse postorder: follow changes through successors in the graph
Strongly connected component (SCC) of a directed graph: path between each two nodes of component.
- compute until fixpoint within each SCC
If we generate control-flow graph from our simple language, what do strongly connected components correspond to?
References
- Principles of Program Analysis, Chapter 6
 , generally
, generally 
 , generally
, generally 