This is an old revision of the document!
Backward VCG: Symbolic Execution using Weakest Preconditions
We again assume for simplicity to have two variables, 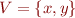 .
.
Rules for Computing Weakest Preconditions
We derive the rules below from the definition of weakest precondition on sets and relations \[
wp(r,Q) = \{ s \mid \forall s'. (s,s') \in r \rightarrow s' \in Q \}
\]
Assume Statement
Suppose we have one variable x, and identify state with that variable. By definition \[ \begin{array}{rl}
wp(\Delta_F,Q) & = \{s \mid \forall s'. (s,s') \in \Delta_F \rightarrow s' \in Q \} \\
& = \{ s \mid \forall s'. (s \in F \land s=s') \rightarrow s' \in Q \} \\
& = \{ s \mid s \in F \rightarrow s \in Q \}
\end{array} \] Changing from sets to formulas (and keeping the same name), we obtain the rule for wp on formulas: \[
wp(assume(F), Q) = (F \rightarrow Q)
\]
Assignment Statement
Consider the case of two variables. Recall that the relation associated with the assignment x=e is \[
x' = e \land y' = y
\]
Then we have, for formula  containing
containing  and
and  :
\[
\begin{array}{rl}
:
\[
\begin{array}{rl}
wp(r_c(x=e),\{(x,y) \mid Q\}) & = \{(x,y) \mid \forall x'.\forall y'.\ x'=e \land y'=y \rightarrow Q[x:=x',y:=y'] \} \\
& = \{(x,y) \mid Q[x:=e] \}
\end{array} \] From here we obtain for formulas: \[
wp(x = e, Q) = Q[x:=e]
\]
Havoc Statement
\[
wp({\it havoc}(x),Q) = \forall x.Q
\]
Sequential Composition
\[
wp(r_1 \circ r_2, Q) = wp(r_1, wp(r_2, Q))
\] Same for formulas: \[
wp(c_1\ ;\ c_2, Q) = wp(c_1, wp(c_2, Q))
\]
Nondeterministic Choice (Branches)
In terms of sets and relations \[
wp(r_1 \cup r_2, Q) = wp(r_1,Q) \cap wp(r_2, Q)
\] In terms of formulas \[
wp(c_1 [] c_2, Q) = wp(c_1,Q) \land wp(c_2,Q)
\]
Size of Generated Verification Conditions
Because of the rule ![Math $wp(c_1 [] c_2, Q) = wp(c_1,Q) \land wp(c_2,Q)$](/w/lib/exe/fetch.php?media=wiki:latex:/img6e17dd894b712147ab6b5031d4f7b2b8.png) which duplicates
which duplicates  , the size can be exponential.
, the size can be exponential.
More information
- Calculus of Computation Textbook, Chapter 5 (Program Correctness: Mechanics)