This is an old revision of the document!
Axioms for Equality
For language  and a relation symbol
and a relation symbol 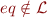 , the theory of equality, denoted AxEq, is the following set of formulas:
, the theory of equality, denoted AxEq, is the following set of formulas:
Definition: if an interpretation 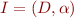 the axioms
the axioms 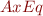 are true, then we call
are true, then we call 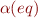 (the interpretation of eq) a congruence relation for interpretation
(the interpretation of eq) a congruence relation for interpretation  .
.
Side remark: Functions are relations. However, the condition above for function symbols is weaker than the condition for relation symbols. If  is a function, then the relation
is a function, then the relation 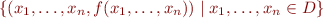 does not satisfy the congruence condition because it only has one result, namely
does not satisfy the congruence condition because it only has one result, namely 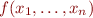 , and not all the results that are in relation eq with
, and not all the results that are in relation eq with 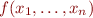 .
.
References
- Calculus of Computation Textbook, Section 3.1
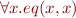
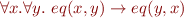
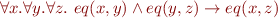
 function symbol with
function symbol with 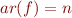 ,
, 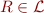 relation symbol with
relation symbol with 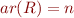 ,
,