This is an old revision of the document!
Axioms for Equality
For language  and a relation symbol
and a relation symbol 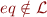 , the theory of equality, denoted AxEq, is the following set of formulas:
, the theory of equality, denoted AxEq, is the following set of formulas:
Definition: if an interpretation 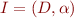 the axioms
the axioms 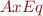 are true, then we call
are true, then we call 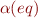 (the interpretation of eq) a congruence relation for interpretation
(the interpretation of eq) a congruence relation for interpretation  .
.
Example: quotient on pairs of natural numbers
Let 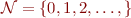 . Consider a structure with domain
. Consider a structure with domain  , with functions
\[
, with functions
\[
p((x_1,y_1),(x_2,y_2)) = (x_1 + x_2, y_1 + y_2)
\] \[
m((x_1,y_1),(x_2,y_2)) = (x_1 + y_2, y_1 + x_2)
\]
Relation  defined by
\[
defined by
\[
r = \{((x_1,y_1),(x_2,y_2)) \mid x_1 + y_2 = x_2 + y_1 \}
\]
is a congruence with respect to operations  and
and  .
.
Congruence is an equivalence relation. What are equivalence classes for elements:
Whenever we have a congruence in an interpretation, we can shrink the structure to a smaller one by merging elements that are in congruence.
In the resulting structure ![Math $([N^2], I_Q)$](/w/lib/exe/fetch.php?media=wiki:latex:/imge1eb6e9867135f1179496cc7a74f7b95.png) we define operations
we define operations  and
and  such that the following holds:
\[
\begin{array}{l}
such that the following holds:
\[
\begin{array}{l}
I_Q(p)( [(x_1,y_1)] , [(x_2,y_2)] ) = [(x_1 + x_2, y_1 + y_2)] \\ I_Q(m)( [(x_1,y_1)] , [(x_2,y_2)] ) = [(x_1 + y_2, y_1 + x_2)]
\end{array} \] This construction is an algebraic approach to construct from natural numbers one well-known structure. Which one?
Note: this construction can be applied whenever we have an associative and commutative operation  satisfying the cancelation law
satisfying the cancelation law  . It allows us to contruct a structure where operation
. It allows us to contruct a structure where operation  has an inverse. What do we obtain if we apply this construction to multiplication of strictly positive integers?
has an inverse. What do we obtain if we apply this construction to multiplication of strictly positive integers?
References
- Calculus of Computation Textbook, Section 3.1
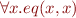
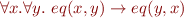
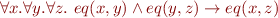
 function symbol with
function symbol with 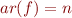 ,
, 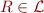 relation symbol with
relation symbol with 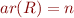 ,
, ![Math $[(1,1)] = $](/w/lib/exe/fetch.php?media=wiki:latex:/img59f2c025571202402b85a56c98961149.png)
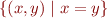
![Math $[(10,1)] = $](/w/lib/exe/fetch.php?media=wiki:latex:/img14c2772767fefb80edd6e518e928c97b.png)
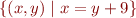
![Math $[(1,10)] = $](/w/lib/exe/fetch.php?media=wiki:latex:/imgd9d71cde6070a9a5af893a771ac75f2d.png)
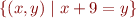
 where
where  is the set of integers.
is the set of integers.