This is an old revision of the document!
Axioms for Equality
For language  and a relation symbol
and a relation symbol 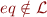 , the theory of equality, denoted AxEq, is the following set of formulas:
, the theory of equality, denoted AxEq, is the following set of formulas:
Note: if an interpretation  satisfies
satisfies 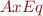 , then we call
, then we call  (the interpretation of eq) a congruence relation for
(the interpretation of eq) a congruence relation for  .
.
Example: quotient on pairs of natural numbers
Let 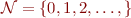 . Consider a structure with domain
. Consider a structure with domain  , with functions
\[
, with functions
\[
p((x_1,y_1),(x_2,y_2)) = (x_1 + x_2, y_1 + y_2)
\] \[
m((x_1,y_1),(x_2,y_2)) = (x_1 + y_2, y_1 + x_2)
\]
Relation  defined by
\[
defined by
\[
r = \{((x_1,y_1),(x_2,y_2)) \mid x_1 + y_2 = x_2 + y_1 \}
\]
is a congruence with respect to operations  and
and  .
.
Congruence is an equivalence relation. What is the equivalence class for element  ?
?
Whenever we have a congruence in an interpretation, we can shrink the structure to a smaller one by merging elements that are in congruence. In the resulting structure we can define operations  and
and  such that the following holds:
\[
\begin{array}{l}
such that the following holds:
\[
\begin{array}{l}
p( [(x_1,y_1)] , [(x_2,y_2)] ) = [(x_1 + x_2, y_1 + y_2)] \\ m( [(x_1,y_1)] , [(x_2,y_2)] ) = [(x_1 + y_2, y_1 + x_2)]
\end{array} \] This construction is an algebraic approach to construct from natural numbers one well-known structure. Which one?
References
- Calculus of Computation Textbook, Section 3.1
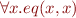
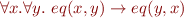
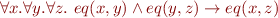
 function symbol with
function symbol with 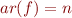 ,
, 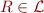 relation symbol with
relation symbol with 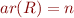 ,
, ![Math $[(1,1)] = $](/w/lib/exe/fetch.php?media=wiki:latex:/img59f2c025571202402b85a56c98961149.png)
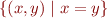
![Math $[(10,1)] = $](/w/lib/exe/fetch.php?media=wiki:latex:/img14c2772767fefb80edd6e518e928c97b.png)
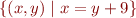
![Math $[(1,10)] = $](/w/lib/exe/fetch.php?media=wiki:latex:/imgd9d71cde6070a9a5af893a771ac75f2d.png)
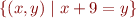
 where
where  is the set of integers.
is the set of integers.