This is an old revision of the document!
Abstract Interpretation Recipe
Program Representation
Control-flow graph: 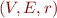 where
where
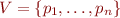 is set of program points
is set of program points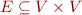 are control-flow graph edges
are control-flow graph edges 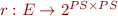 , so each
, so each 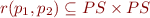 is relation describing the meaning of command between
is relation describing the meaning of command between 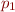 and
and 
We can define meaning of program in this form using Collecting Semantics.
Summary of key steps
- design abstract domain
 that represents sets of program states
that represents sets of program states - define
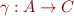 giving meaning to elements of
giving meaning to elements of 
- define lattice ordering
 on
on  such that
such that 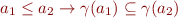
- define
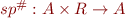 that maps an abstract element and a CFG statement to new abstract element, such that
that maps an abstract element and a CFG statement to new abstract element, such that 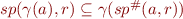
(for example, by defining function  so that
so that 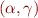 becomes a Galois Connection on Lattices)
becomes a Galois Connection on Lattices)
- extend
 to work on control-flow graphs, by defining
to work on control-flow graphs, by defining 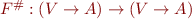 as follows (below,
as follows (below,  )
)
\[
F^{\#}(g^{\#})(p_2) = g^{\#}(p_2) \sqcup \bigsqcup_{(p_1,p_2) \in E} sp^{\#}(g^{\#}(p_1),r(p_1,p_2))
\] which is analogous to Collecting Semantics
- compute
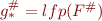 (this is easier than computing collecting semantics because lattice
(this is easier than computing collecting semantics because lattice 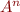 is simpler than
is simpler than  ):
):
\[
g^{\#}_* = \bigsqcup_{n \ge 0} (F^{\#})^{n}(\bot^{\#})
\]
where 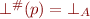 for all
for all 